この問題は、根を含む乗法と根を含む除法の2つを組み合わせた式になります。 この計算手順は、 乗法・除法を"根を含まない式と同様に計算する。 素因数分解を実行し、根の外に出せる値があれば出す。 分母に根がある場合は、有理化する。根号を含む数は \(1\) つの文字とみなし、文字式と同じ方法で計算します。したがって、根号を含む数の加法と減法において、式を展開する場合も多項式と同じように 分配法則 や 乗法公式 を利用して展開することができます。※計算の結果、根号の中の数字が2乗の形になっていると、根号を外せます。教科書 p30 下段の「根号を含む式の計算」公式1を使いましょう。 (1)、(2)の計算問題は、教科書p7 「プレリュード 8 根号を含む式の乗法・除法」に対応する出題です。教

中3 中3 数学 根号を含む式の計算 中学生 数学のノート Clear
根号を含む式の計算 問題
根号を含む式の計算 問題-2 根号をふくむ式の計算 ・1・ 根号をふくむ式の乗法、除法 全4時間 1/4時 ねらい ・ 根号をふくむ式の乗法、除法について理解する。 教科書45ページの練習問題①②③を考える。平方根の大小関係を不等号で表す問題を解説! 根号を含む式の値の求め方とは?←今回の記事 分母の有理化のやり方はこれでバッチリ! ルートの計算方法まとめ!問題を使って徹底解説! ルートの分数計算、問題解説で完全マスターだ!




根号を含む式の計算 の問題のわからないを5分で解決 映像授業のtry It トライイット
各単元の「問題一括」または「解答一括」をクリックすると、新しいウィンドウ(またはタブ)にPDFファイル が表示されます。 保存または直接印刷してください。 式の計算 多項式と単項式の乗除(1) 根号を含む計算次 69 三角関数の有理式の積分 上 6 積分法 前 67 有理関数の積分 6 8 根号を含む関数の積分 注意 6 44 (根号を含む場合の計算) 関数 に根号 を含む場合の 不定積分を考える. 変数変換 とおき置換積分法で求積する.・根号を含む式の加法と減法について計算が正しくできるようになろ う。 根号を含む式の加法と減法の計算では、同類項をまとめるようにして、同じ数の平方 根を含んだ項をまとめていきます。 ※今日の学習のポイント 中学校3年 数学 ※根号を含む式の
根号を含む式の計算 by omusoshiru 公開 19年5月30 日 更新済み 19年5月30 根号を含む式から根号を取り除く式変形。 問題 / 数と式 / 数学A /第3講:2重根号(解答) Tweet 基本問題, 定期テスト, 確認テスト, 練習問題 第2講 根号を含む式の計算(1章 2節実数)問題集高校数学Ⅰ 1講 不等式の性質(1章 3節1次不等式)問題集高校数学Ⅰ第2講 根号を含む式の計算(1章 2節実数)問題集高校数学Ⅰ です。わかりやすいポイントと例題つきの問題集です!練習問題と確認テストもついてますよ!定期テスト対策にお使いください。全て無料でダウンロードできます。塾や家庭教師、学校でご自由にお使いください!
一方、「根号を使わず」という問題は、 純粋な計算問題なので、 書いてある通りの数値を、 計算すればOKです。 この点の違いを押さえるのがコツですね! 「根号を使わずに表しなさい。」とは? では、例題を見てみましょう。 平方根の加減法の計算問題です。計算のやり方基本平方根の加減法は同じ数の平方根を含んだ式を、同類項をまとめるときと同じようにして計算します。例)math3\sqrt { 5 } 4\sqrt { 5 } =7\sqrt { 5 } /math根号を含む数の変形、分母の有理化をしてから計算します。根号を含む式の値の求め方とは? 分母の有理化のやり方はこれでバッチリ! ルートの計算方法まとめ! 問題を使って徹底解説! ルートの分数計算、問題解説で完全マスターだ! ←今回の記事 整数部分、小数部分の求め方! 分数の場合には?




ルート計算 展開公式をつかう3つの平方根問題の解き方 Qikeru 学びを楽しくわかりやすく



1
根号を含む式の計算 by omusoshiru 公開 19年5月30日 更新済み 19年5月30日 1根号を含む式の乗法・除法== 根号計算の入試問題 == 根号を含む分数が幾つもある場合,通分よりも分母の有理化の方が有利 類題 を計算せよ. 解説 やり直す 引用元の問題は記述式の問題ですが,以下の問題ではWeb画面上での操作性をよくするため,選択問題に変えています練習問題 1111 根号を含む式の計算根号を含む式の計算 次の計算をしなさい。 (1) 18 50 − 8 (2) 3 5− 125 (3) −3 48 4 3− 75 (4) 2 24 − 54 2 6 (5) − 45 6 5− −2 (6) 175 −2 28 − 63 4 2 (7) − 2 1− 8 8 (8) 35 14 − 28 10 5 (9) 5 2 3−2 − 1− 12 (10) 15 27 − 5 3 60 2




ルート 根号 の計算方法をマスターしよう スタディクラブ情報局




根号を含む式の計算 の問題のわからないを5分で解決 映像授業のtry It トライイット
7 根号ふくむ式の 計算 根号をふくむ 式の乗除(1) (関)根号をふくむ式の四則に関心を持 つ。 (技)根号をふくむ式の乗除を計算するこ とができる。 観察 発言 ノート 8 根号をふくむ 式の乗除(2) (技)公式を利用して数を変形することが 当たり前のように思える、ルートどうしのかけ算・割り算の公式。この公式が成り立つことを証明します。 Ⅰ 根号を含む式の乗除 Ⅱ 具体数による確認 Ⅲ 証明 Ⅰ 根号を含む式の乗除 中学3年122 根号を含む式の計算 14 集合と命題 141 集合 142 命題と条件 143 命題と証明 14問題 1演習問題




中3数学 平方根 3 6 根号を含む式の加減 Youtube




根号を含む式の計算 の問題のわからないを5分で解決 映像授業のtry It トライイット
平方根整数 (入試問題) → 携帯版は別頁 == 根号計算の入試問題 == ※以下に引用する高校入試問題で,元の問題は記述式の問題ですが,web画面上で入力問題にすると操作性が悪いので,選択問題に書き換えています. 問題1 (画面上で解答するには 中学3年数学 平方根 根号を含む式の計算 練習問題5・解答 エネルギー 中学3年理科 生物の細胞と生殖 細胞と生物の成長 確認問題1・解答ここでは、根号を含む式の計算について解説します。具体的には 1 基本的な問題、 2 根号の外し方に注意がいる問題、 3 二重根号の問題 を解いていきます。




この公式の証明がしたいのですが わからないので教えてほしいです Clear




根号を含む式の計算 の勉強法のわからないを5分で解決 映像授業のtry It トライイット
② 根号を含む簡単な式の計算をすることができる。 ③ 有理数と無理数の意味及び数の集合について理解することができる。 ④ 具体的な場面で数の平方根を用いて表したり処理したりすることができる。 中学3年数学 平方根 根号を含む式の計算 1、平方根の乗法・除法 平方根の積と商 正の数a,bについて √a×√b=√a×b √a/√b=√a/b が成り立ちます。 √ の外にある数を,√ の中に入れることができます。 正の数a,bについて、a√b=√a²b と変形する正の数の平方根を含む簡単な式の計算ができるようにする。 2 素因数分解 基本の問題 2時間 3 根号をふくむ式の乗除 4時間 4 根号をふくむ式の加減 2時間 5 根号をふくむ式のいろいろな計算 1時間 6 平方根の利用(本時) 1時間




この問題で 5を証明するのがわかりません Clear




平方根 ルートの計算方法まとめ 問題を使って徹底解説 数スタ
2重根号の計算|数学|苦手解決q&aのページです。 数と式絶対値記号を含む方程式・不等式の解き方 19年12月17日に21年度「大学入学共通テスト」にて予定されていた国語・数学の記述式問題の導入見送りの発表が文部科学省よりございました。問次の式を計算せよ。101~ (2) √2+√32-√72=254~ (3) (2√5+3√6)-(√96-√45)=519~ (4) (2√3-√6) (√3+3√6)=9A 3 1 7 5 7 35 数学32章平方根「平方根を含む式の計算」<準備問題②> 組 番 名前 1次の数を変形して, の形にしなさい。




中学 数学 こういう問題の時答えの順番が反対になってしまっても丸です 数学 教えて Goo




平方根 ルート の重要な計算方法まとめ 数学fun
②根号を含んだ式の四則の計算方 ②根号を含む式の計算に興則、結合法則が成り立つことを考える②根号の中の数を外に出したり、そ法や手順を理解する。 味・関心を持ち、すすんでことができる。 の逆の変形をしたりすることができ③根号を含む式の 今回は平方根の計算を学ぶ。 定期テストレベルでは、今回までの内容ができれば、 平方根の分野で平均点以上を取れる。 公立高校入試では、大問1の小問集合などでよく出るので、 確実に得点できるようにしておこう。 前回 ←平方根の計算の準備(基) 次回 →平方根の計算(標)中3 数学の基本問題 中3 式の計算 単項式と多項式の乗除 PDF 答え付き 多項式の乗法 (ab) (cd) PDF 答え付き 展開 乗法の公式 1 (xa) (xb) PDF 答え付き



3



ルートの分数計算 問題解説で完全マスターだ 数スタ
根号を含む式の計算 無理数でも根号を使って表す無理数と\(\,\pi\,\)などの根号を使わない数があります。 根号(ルート)を使った計算は中学でもやっていますが、 数学\(\,\mathrm{Ⅰ}\,\)での無理数計算は分数計算や求値問題が主な内容です。中3数学で学ぶ「ルートの計算とカッコ×カッコの公式」のテストによく出る問題(練習)を学習しよう! 根号を含む式の計算の問題を見る > すべての授業の「要点まとめノート」「問題・解答」をPDF無料ダウンロードできる 学校で使っている教科書に根を含む簡単な式の計算ができるようにする。 具体的な場面として、高知県数学思考力問題集「紙の規格を調べよう(3-2-b)」を活用し、b4 判の紙はb5 判の紙と比 較して、縦の長さと横の長さがそれぞれ何倍になるかを説明させる。




平方根の計算 平方根のチョー簡単な問題をまとめたよ 三重の個人契約家庭教師




高校 数学 数と式32 根号の加減法 11分 Youtube
技能を問う問題になっている。例えば、文字式に根 号を含む数を代入する問題や根号の中の数を自然 数にする問題である。すべての都道府県の高校入試 問題には、根号を含む基礎的な計算問題もしくは基 礎的な知識・技能を問う問題が必ず含まれている。 平方根の加減法の計算問題です。 計算のやり方基本 平方根の加減法は 同じ数の平方根を含んだ式を、同類項をまとめるときと同じようにして計算します。 例) 根号を含む数の変形、分母の有理化をしてから計算します。 例) ポイ




中学数学 式の計算の利用 ママ塾ノート




平方根の計算 平方根のチョー簡単な問題をまとめたよ 三重の個人契約家庭教師



Studydoctor根号 ルートと式の値 中3数学 Studydoctor




第2講 根号を含む式の計算 1章 2節実数 問題集 高校数学




根号を含む式の計算 積 商と の変形 教遊者




根号を含む式の計算 しっしーのお計算ん向上委員会




中3 授業 中3数学 平方根の計算 中学生 数学のノート Clear




根号を含む式の計算 一夜漬け高校数学311 ルートの計算 練習問題 Youtube
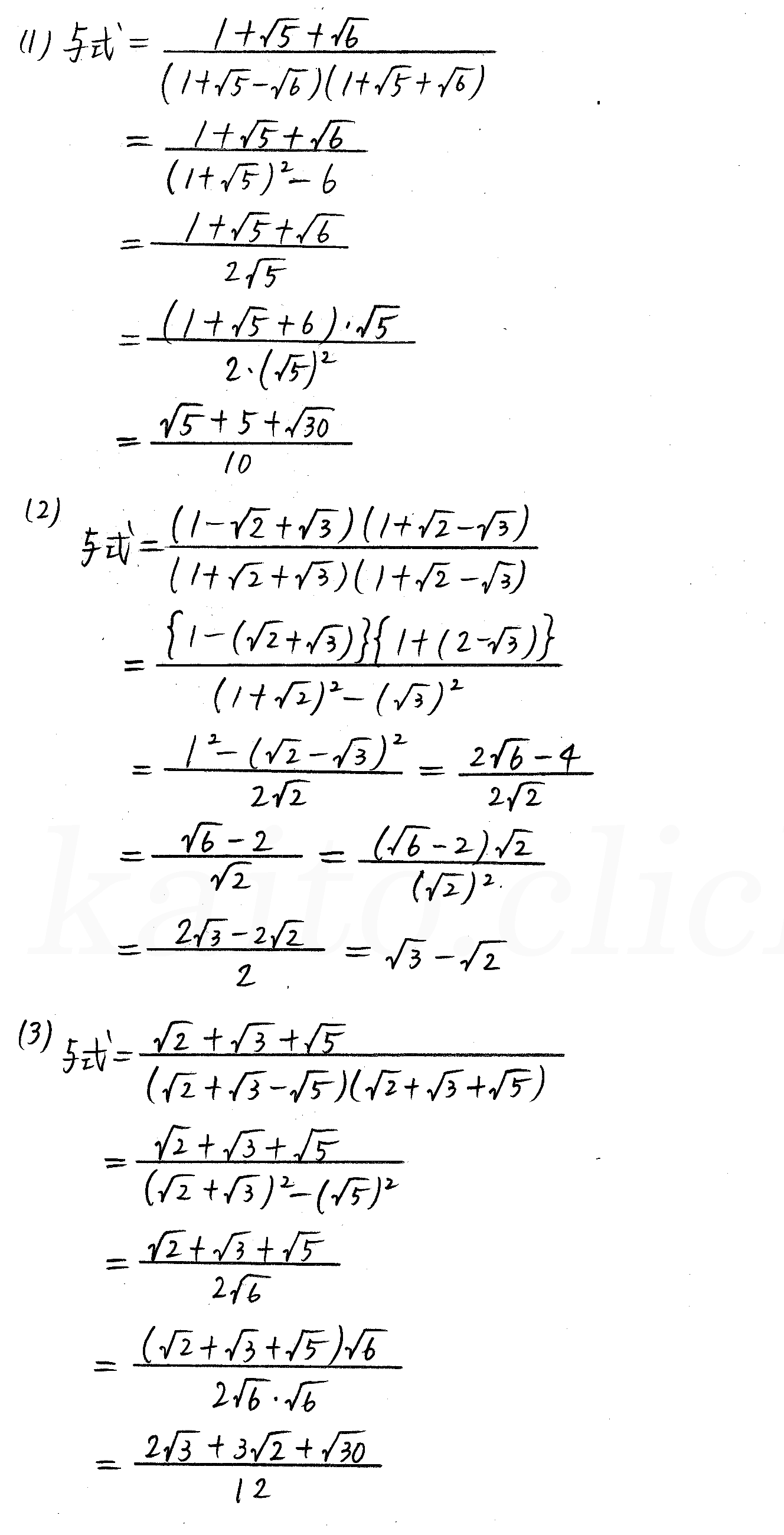



改訂版 クリアー数学 P 7 根号を含む式の計算




心に強く訴える中3 数学 ルート 問題 最高のカラーリングのアイデア




第2講 根号を含む式の計算 1章 2節実数 問題集 高校数学




平方根 平方根の加法 減法 乗法 除法 中学数学 定期テスト対策サイト
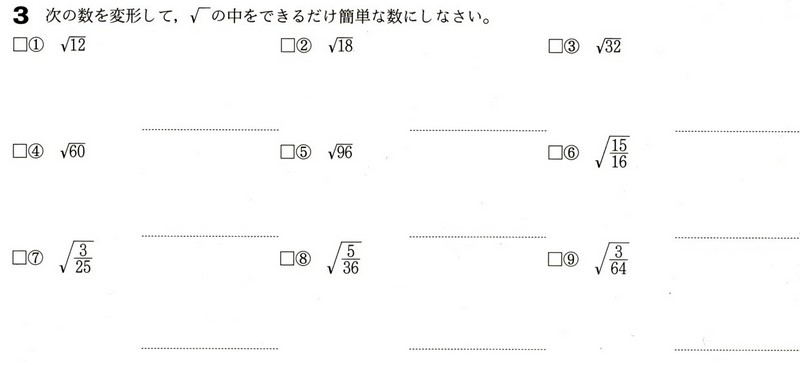



中学3年数学 平方根 根号を含む式の計算 練習問題3 あんのん塾



3 36第2章12平方根の計算 根号を含む式の乗法 フロントエンドなブログ
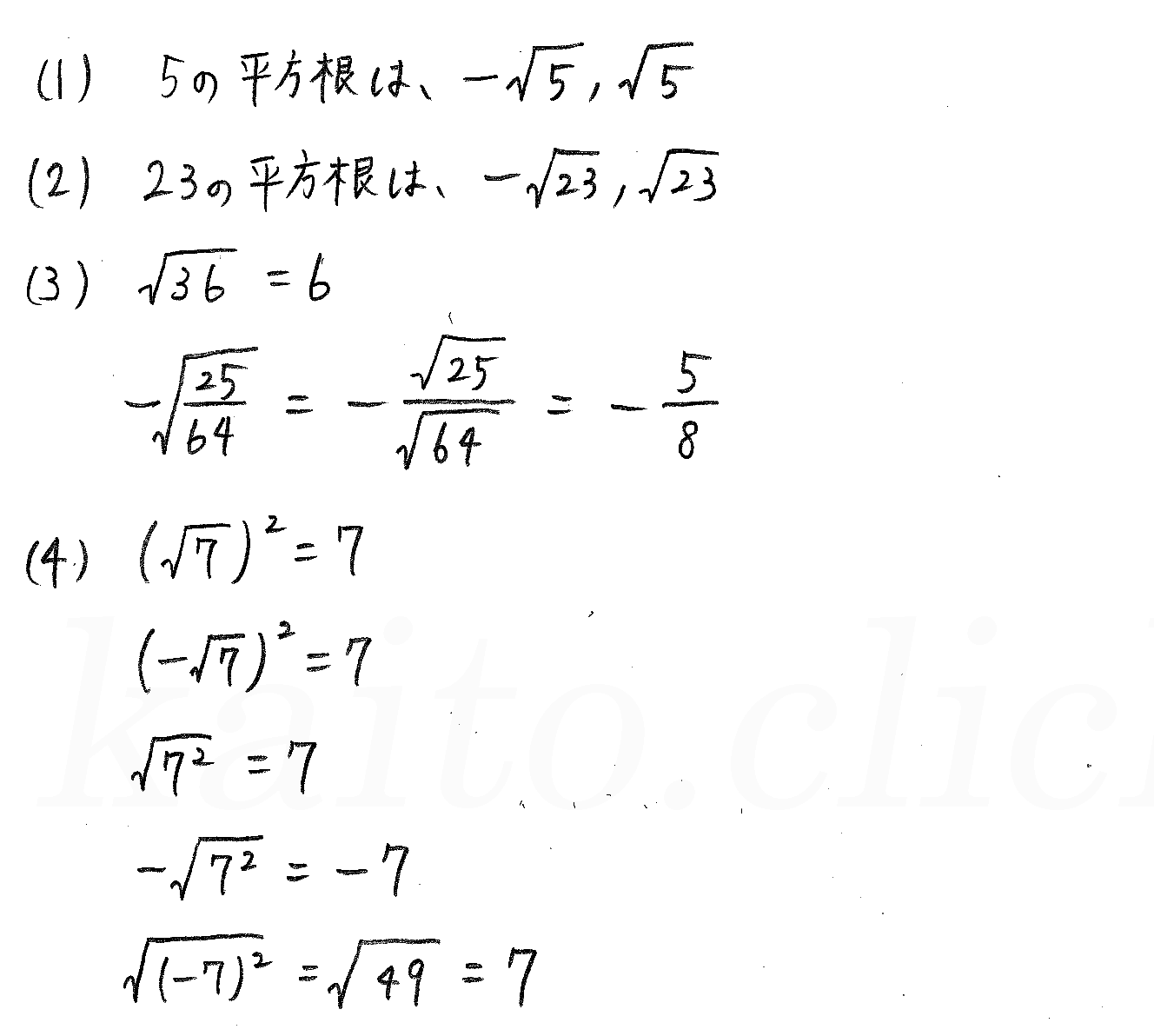



改訂版 3trial数学 P17 5 根号を含む式の計算




根号を含む式の計算 一夜漬け高校数学311 ルートの計算 練習問題 Youtube



平方根の割り算は 1分でわかる計算 割り算の問題とやり方 有理化 分数との関係




4step 数 1 5 根号を含む式の計算 問題番号60 Youtube




根号を含む式の計算 の問題のわからないを5分で解決 映像授業のtry It トライイット




平方根 加減法 無料で使える中学学習プリント



根号を含む式の計算です なぜこの答えが間違ってるのか分かりま Yahoo 知恵袋




中3 平方根 根号を含む式の計算 積 商と の変形 デジタル板書データ Youtube




平方根の計算 平方根のチョー簡単な問題をまとめたよ 三重の個人契約家庭教師




中3数学 平方根 24 中学数学高校数学個別指導in山形市 数専ゼミ




中学3年数学 平方根 根号を含む式の計算2 確認問題2 あんのん塾




平方根 ルート の足し算と引き算のやり方と計算問題 中学3年生数学 Irohabook
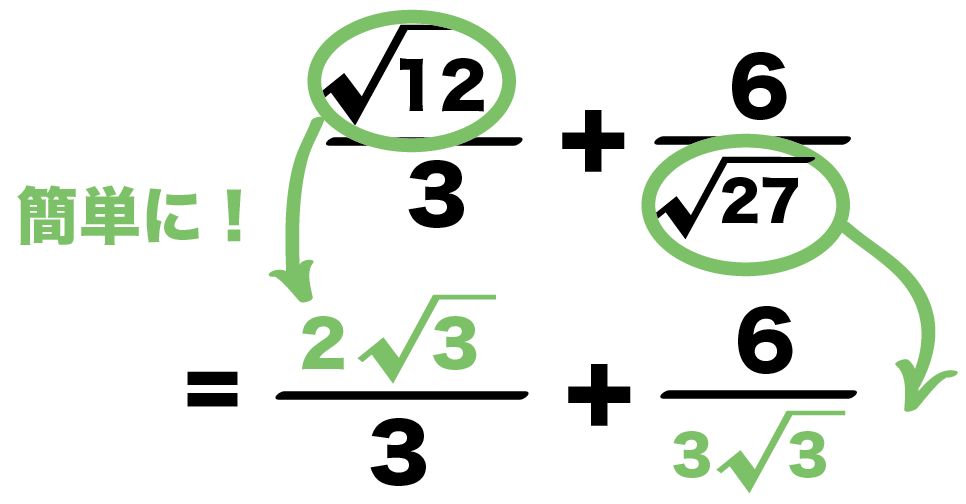



平方根の計算 ルートの分数の足し算 引き算の仕方がわかる5ステップ Qikeru 学びを楽しくわかりやすく




中学数学 平方根の利用 ママ塾ノート




根号と分配法則 Youtube




根号を含む式の計算 しっしーのお計算ん向上委員会




平方根とは 東大生が平方根の計算方法や覚え方を伝授 高校生向け受験応援メディア 受験のミカタ
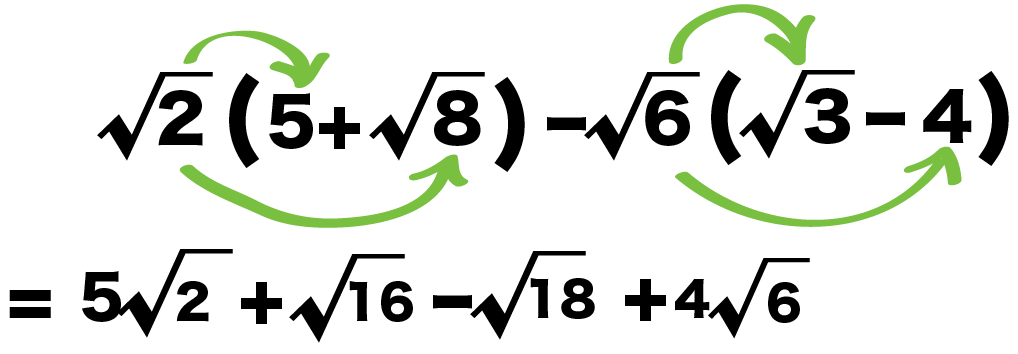



平方根の式を分配法則で計算する4つのステップ Qikeru 学びを楽しくわかりやすく




中3 9 1 根号を含む式の加法 減法の計算 Youtube




中学3年生 数学 平方根のいろいろな計算 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中学3年生 数学 平方根の乗法 除法 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




ルートの分数計算 問題解説で完全マスターだ 数スタ




中学3年数学 平方根 根号を含む式の計算 練習問題14 あんのん塾
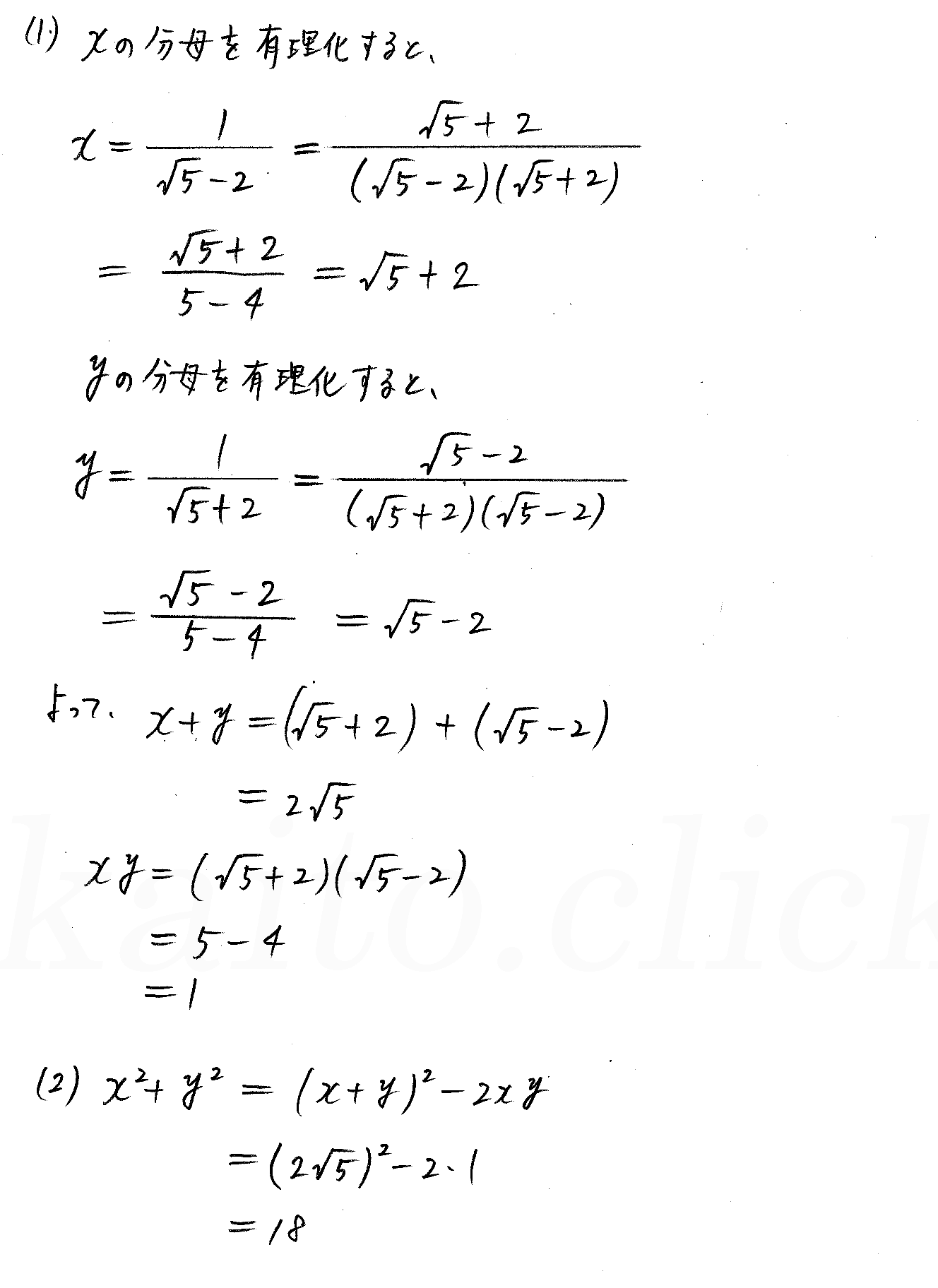



改訂版 4プロセス数学 P19 5 根号を含む式の計算
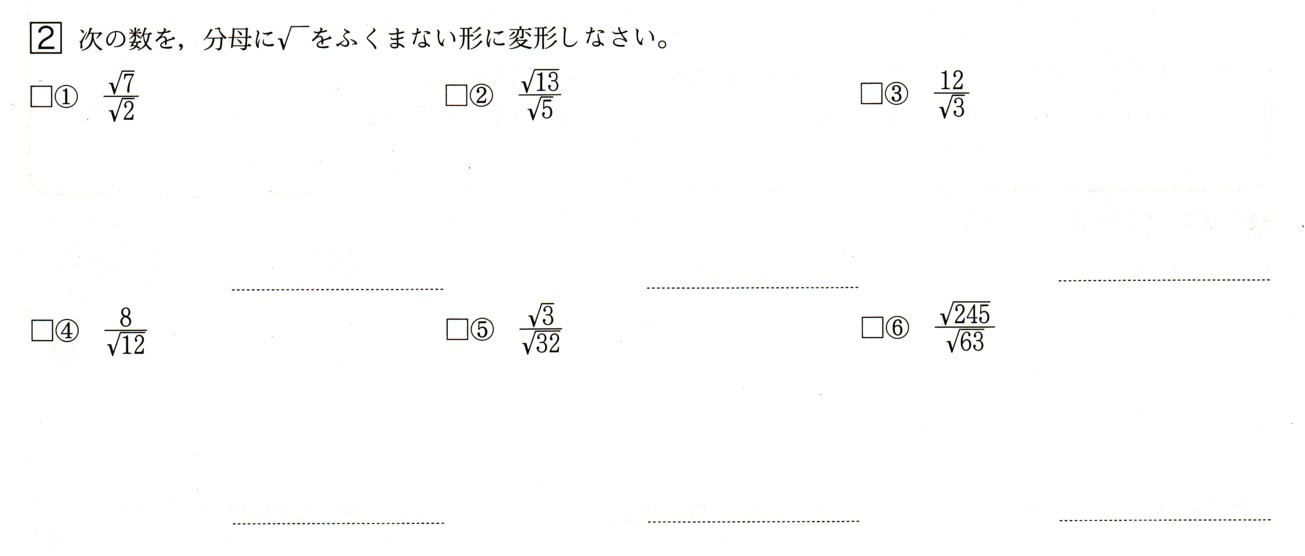



中学3年数学 平方根 根号を含む式の計算 確認問題2 あんのん塾




有理化とは やり方を分かりやすく解説 練習問題つき 高校生向け受験応援メディア 受験のミカタ




中3数学 平方根 31 中学数学高校数学個別指導in山形市 数専ゼミ
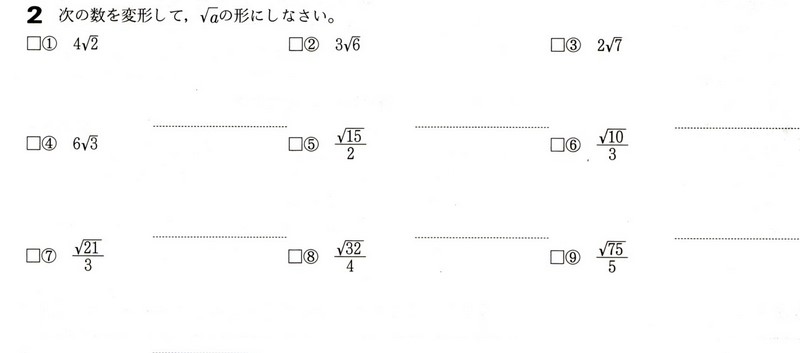



中学3年数学 平方根 根号を含む式の計算 練習問題2 あんのん塾




第2講 根号を含む式の計算 1章 2節実数 問題集 高校数学




中学校数学自宅学習3年 根号を含む式の計算



1




根号を含む式の計算 の問題のわからないを5分で解決 映像授業のtry It トライイット



数iの根号を含む式の計算です 問2なのですが 公式4 5 Yahoo 知恵袋



平方根の計算 平方根のチョー簡単な問題をまとめたよ 三重の個人契約家庭教師




中学3年生 数学 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




根号




改訂版 4step数学 P17 5 根号を含む式の計算




根号を含む式の問題が分かりません 教えて下さい Clear




根号を含む式の計算 積 商と の変形 教遊者




中3 数学 無料学習プリント教材




中学3年生 数学 平方根の乗法 除法 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




第2講 根号を含む式の計算 1章 2節実数 問題集 高校数学




平方根 ルート の足し算と引き算のやり方と計算問題 中学3年生数学 Irohabook




中3 平方根 を含む式の和と差 日本語版 Youtube



1
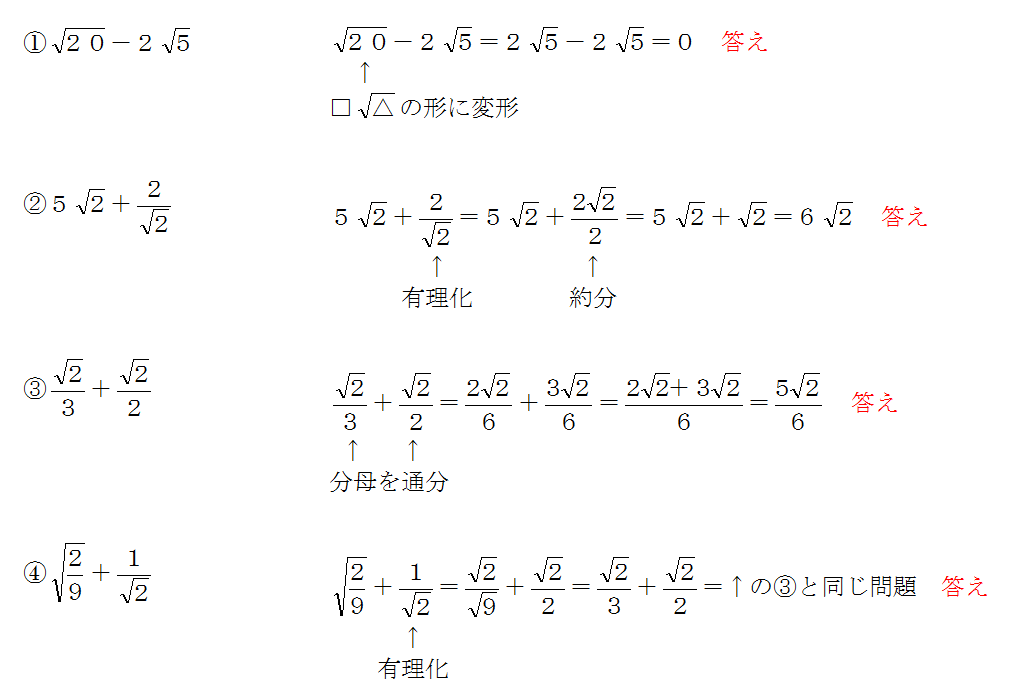



平方根の計算 平方根のチョー簡単な問題をまとめたよ 三重の個人契約家庭教師
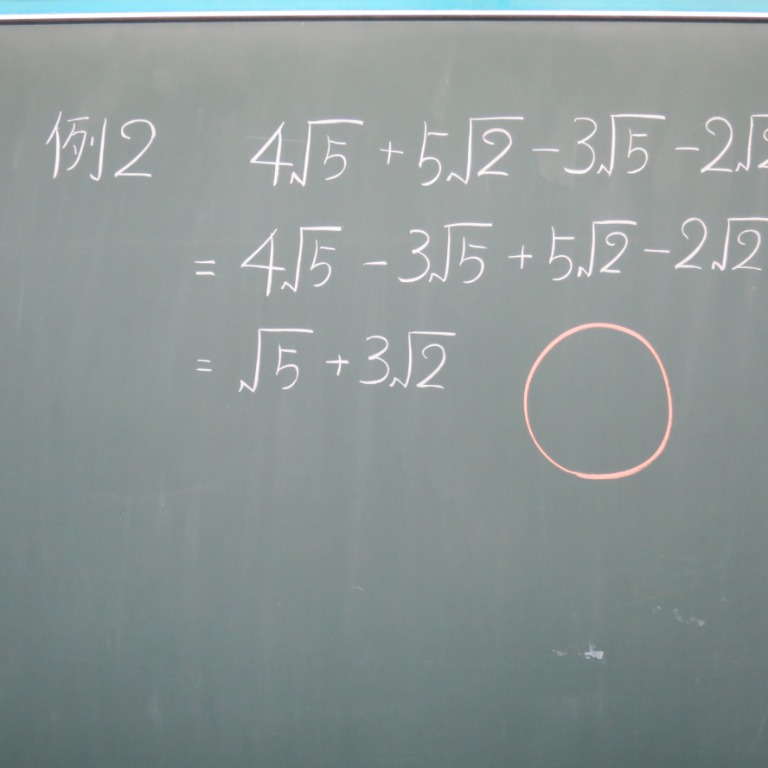



Tossランド 根号を含む式の加減




中学3年生 数学 平方根の乗法 除法 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




第2講 根号を含む式の計算 1章 2節実数 問題集 高校数学




平方根 式の値 求め方はどうやる 問題を使って徹底解説 数スタ
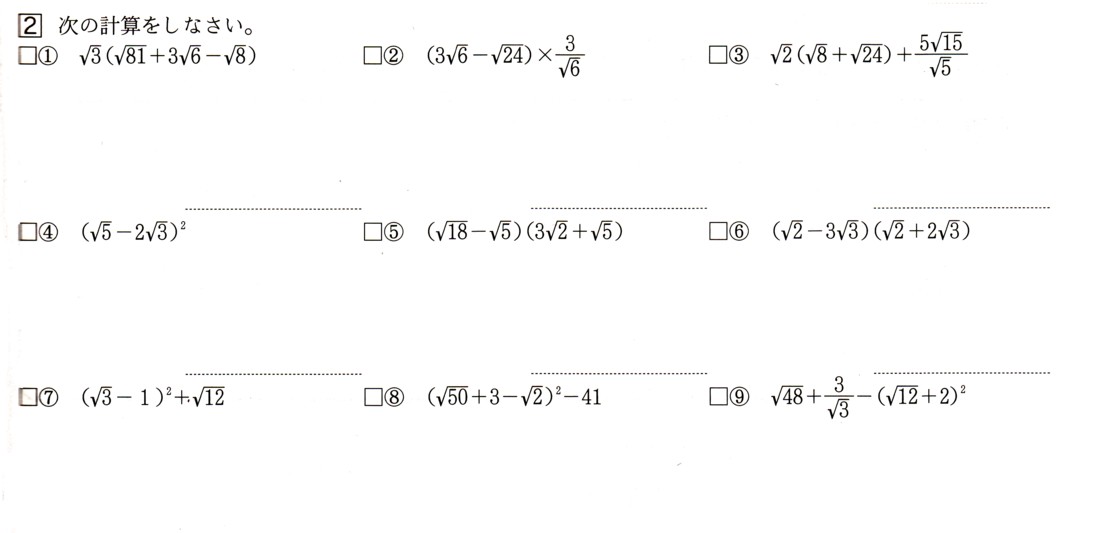



中学3年数学 平方根 根号を含む式の計算 3確認問題2 あんのん塾




高校 数 根号の式を含む計算2 Youtube




Youtube Lesson 中3 平方根 第6回 根号を含む式の計算 和と差 桂坂数学教室




中3 数学 無料学習プリント教材



高校数学i根号を含む式の計算 この問題の 1 の解き方をいくら調べ Yahoo 知恵袋




高校1年生の数1の問題です Clear
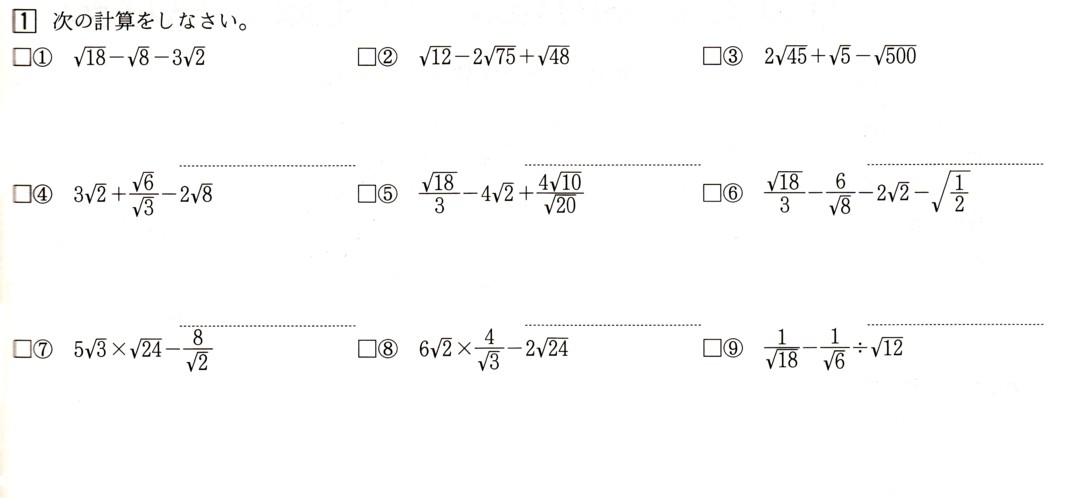



中学3年数学 平方根 根号を含む式の計算 3確認問題1 あんのん塾




第2講 根号を含む式の計算 1章 2節実数 問題集 高校数学




平方根 A B の形に変形するやり方とは 問題を使って徹底解説 数スタ




中学3年数学 平方根 根号を含む式の計算 練習問題9 あんのん塾




平方根 加減法 無料で使える中学学習プリント




複雑なルートの分数の有理化のやり方と問題 理系ラボ



平方根 ルート の計算や問題の解き方を完璧に理解しよう Studyplus スタディプラス




根号をふくむ足し算と引き算 の分数をふくむ場合 Youtube




第2講 根号を含む式の計算 1章 2節実数 問題集 高校数学




中学3年生 数学 平方根のいろいろな計算 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中3 中3 数学 根号を含む式の計算 中学生 数学のノート Clear




中学校数学3年 根号を含む式の和と差 根号を含む式の積 Youtube




Kelas 11 Catatan Tentang 根号を含む式の計算 重点だけ Clear



Www Yashima Ac Jp Okinawa Pdf Home Learning 0451 Pdf




中学数学3年 いろいろな平方根の計算 平方根と式の値 受験の月




中学数学 平方根の利用 ママ塾ノート




高校数学 平方根の定義と2乗の平方根 A の基本的な扱い 受験の月
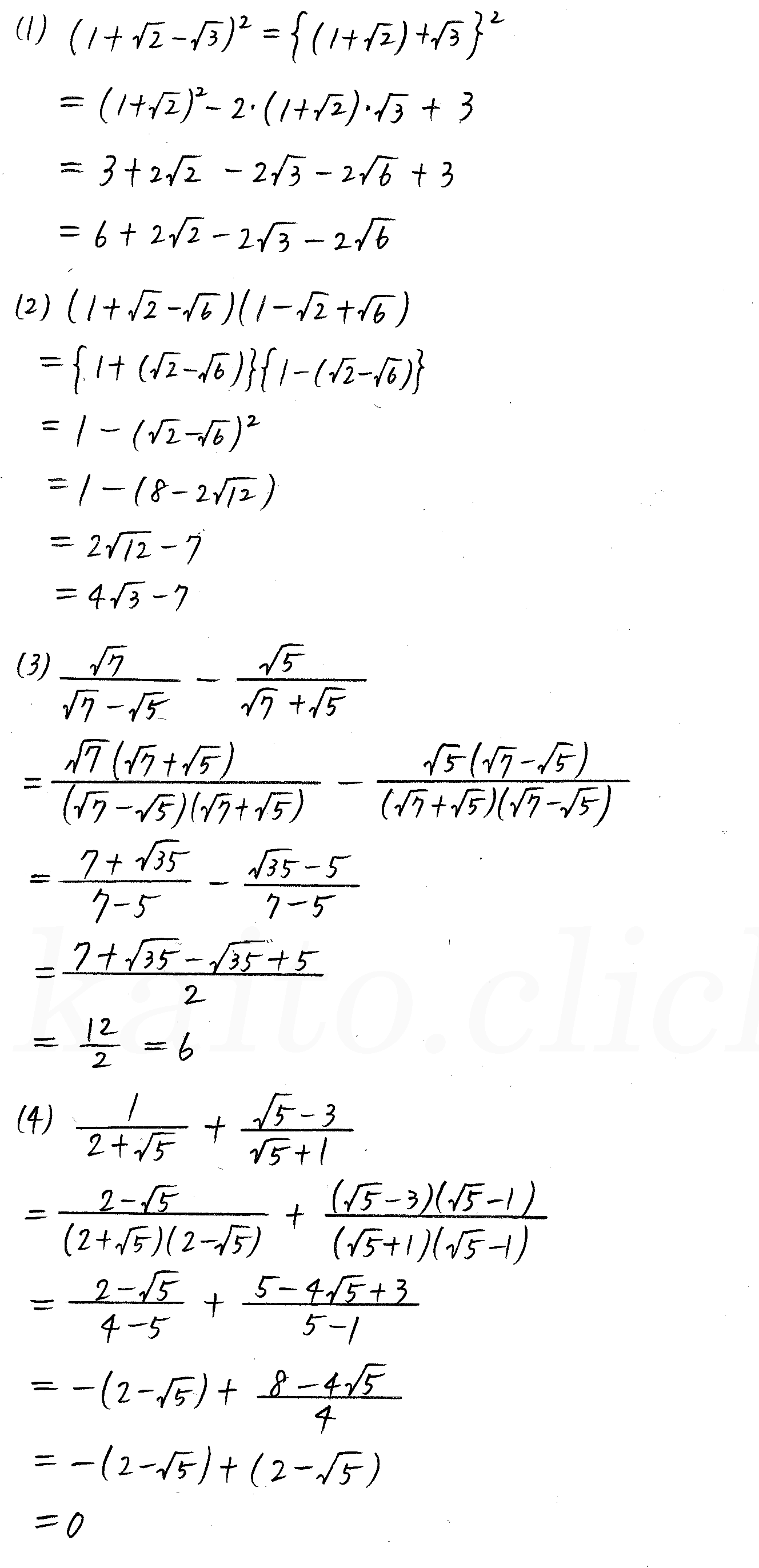



改訂版 クリアー数学 P19 7 根号を含む式の計算



0 件のコメント:
コメントを投稿