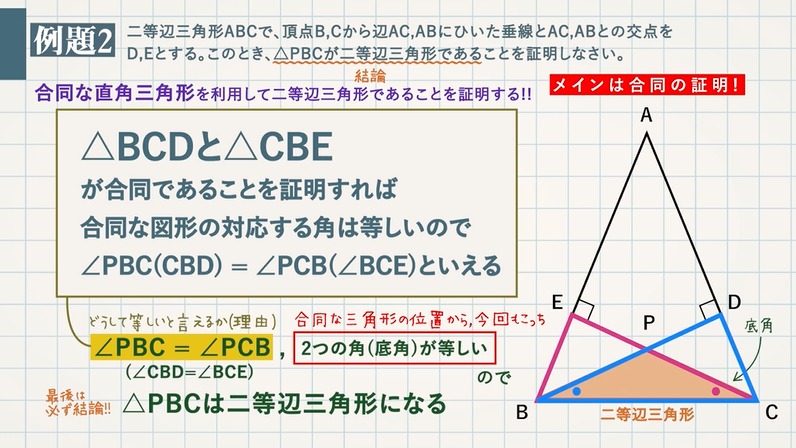
{AC=BC}の二等辺三角形}$2点(x_1,\ y_1),\ (x_2,\ y_2)間の距離 \ruizyoukon{(x_2x_1)^2(y_2y_1)^2} \\2zh 実際には,\ \ruizyoukon{ }\,が鬱陶しいので辺の長さの2乗を考える \\1zh また,\ \bm{直角三角形であることの必要十分条件は三平方の定理が成り立つこと}である \\2zh よっ二等辺三角形 足が5本(正五角形? )の椅子を購入することを考えてます。 足の横幅で、最長の幅は記載があるが、最小の幅の記載がない。 がないため2等辺三角形の高さが最小幅と考えネットで公式はたくさん出てくるが自分で計算できなかったのでお二等辺三角形になるための条件(定理) 二つの角が等しい三角形は、それらの角を底角とする二等辺三角形である。 この条件は(定理)でもあるから、もちろん二等辺三 角形の定義から証明して導くことができるんだ。

二等辺三角形の定理の証明がわかる3ステップ Qikeru 学びを楽しくわかりやすく
二等辺三角形の条件
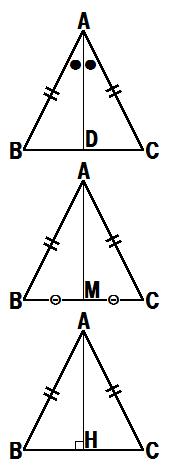
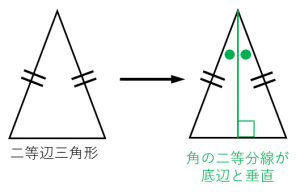
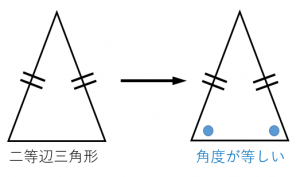
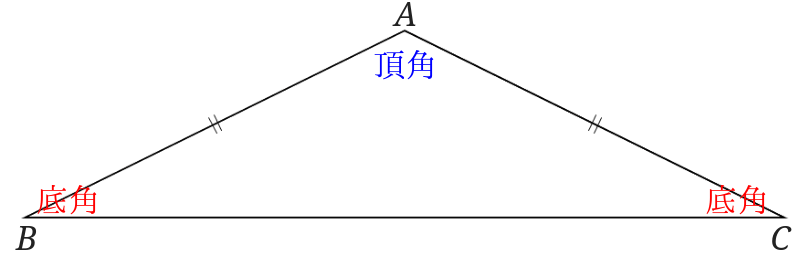
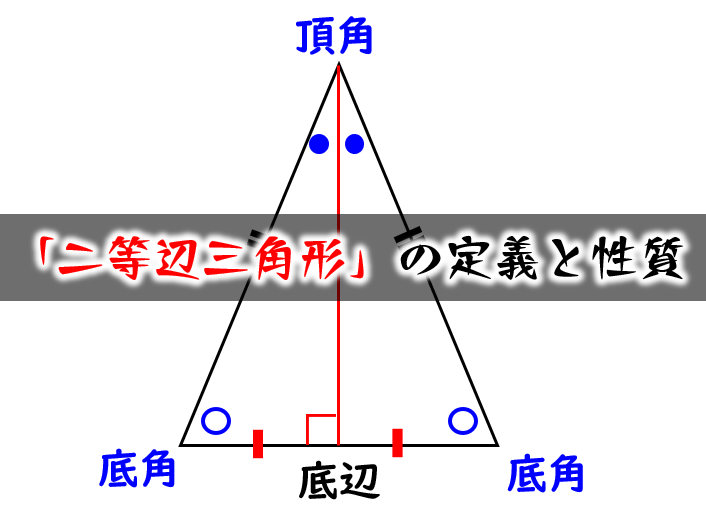
二等辺三角形の条件-②二等辺三角形の性質 ⑴二等辺三角形の2つの底角は等しい。 ⑵二等辺三角形の頂角の二等分線は、底辺を垂直 に二等分する。 ③二等辺三角形になるための条件 2つの角が等しい三角形は、二等辺三角形である。 $ % 底辺 頂角 底角 3 特別な二等辺三角形二等辺三角形になるための条件(1) 二等辺三角形になるための条件 定理 三角形の2つの角が等しければ、その三角形は等しい2つの角を底角 とする二等辺三角形である。 1 下の図のように、AB=ACの二等辺三角形ABCの辺AB,AC上にそれぞれ
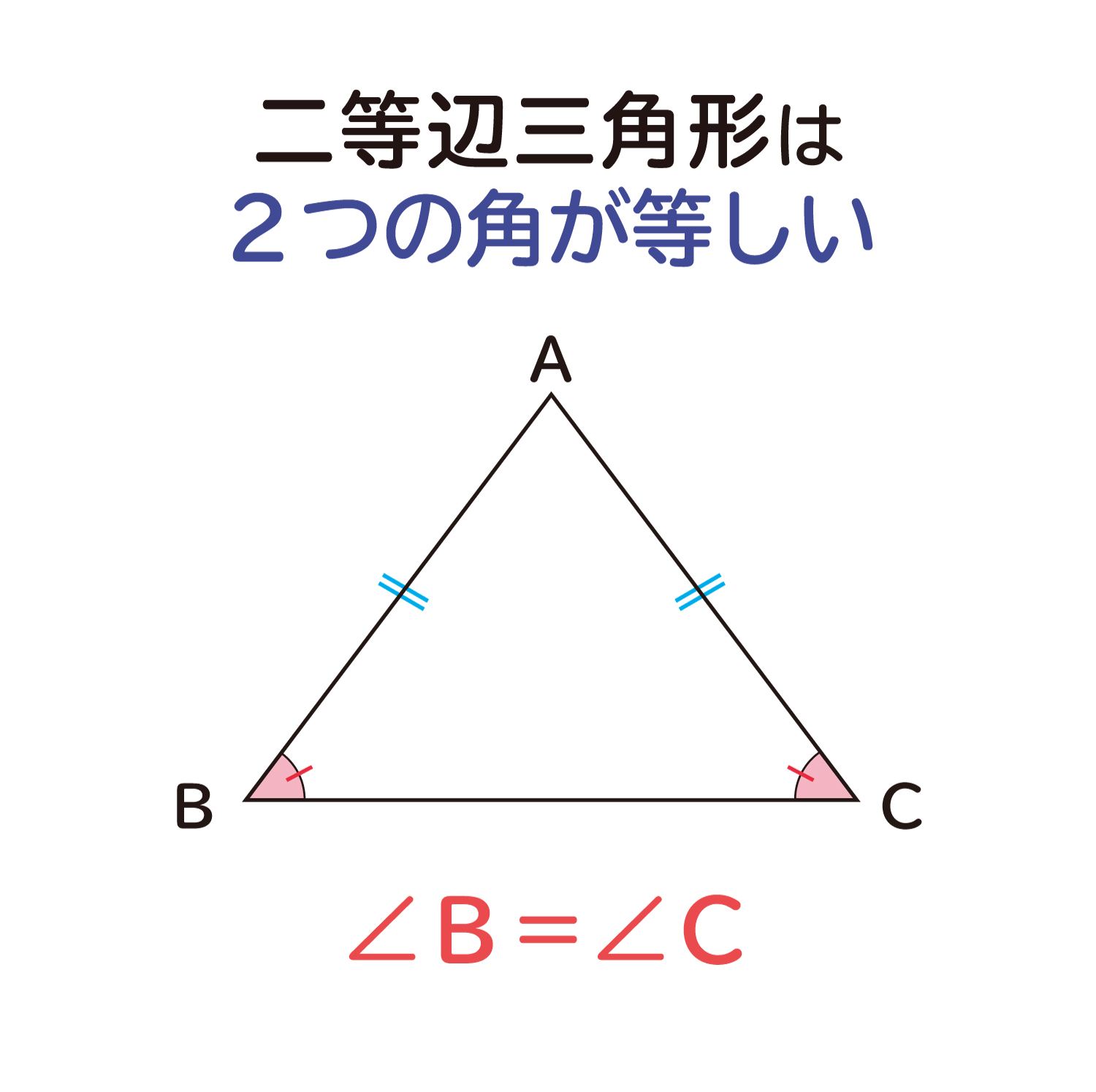



二等辺三角形の2つの角は等しくなる ことの説明 おかわりドリル
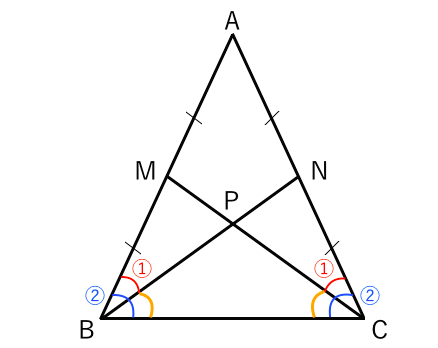
正十一角形の頂点から $3$ つの頂点を選んでつくられる二等辺三角形全体を考えます.仮定より,二等辺三角形は『すべての頂点が同色』か,『$2$ 点が同じ色で,残りの $1$ 点が異なる色』であるような $2$ つのパターンに分けられます.二等辺三角形 の性質 ・二等辺三角形のいろいろな性質に関心を持 ち,それらを証明しようとしている。 ・二等辺三角形,正三角形の定義や性質を理 解している。 活動観察 課題プリント 定期テスト 3 4 二等辺三角形 になるための 条件 ( 本 時 )ア~カの中から,二等辺三角形を3つ選んで,記号をかきなさい。 ( ) ( ) ( ) 2 2~4について, 空欄をうめて,証明を完成させなさい。 2つの角が等しい三角形は,二等辺三角形である (二等辺三角形の条件) 証明 頂角aの二等分線adをひく abdと において,
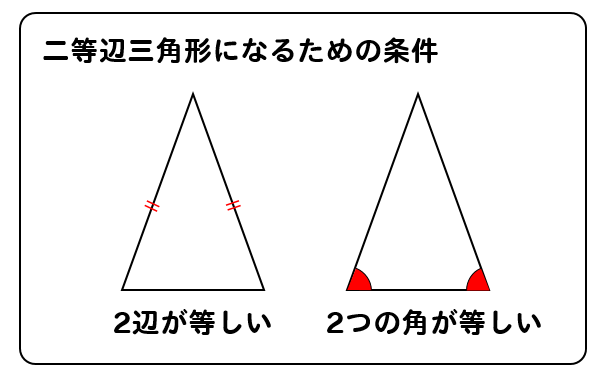
二等辺三角形の合同条件を教えてください!! 二等辺三角形の定義 二辺の長さが等しい三角形 二等辺三角形の性質 ①二等辺三角形の2つの底角は等しい。 ②二等辺三角形の頂角の二等二等辺三角形 になるための 条件 二等辺三角形に なるための条件 を考察し,証明す ることができる。 ある定理の逆を いうことができ, それが成り立つ かどうかを調べ ることができる。 定理の逆の意味を 理解している。 二等辺三角形にな るための条件直角二等辺三角形の辺の比は「三平方の定理」から導くことができます。 直角二等辺三角形の底辺と高さの長さは同じです。 底辺(高さ)の長さを「1」として、三平方の定理に代入すると「斜辺 2 =底辺 2 高さ 2 ⇒ 斜辺 2 =11=2 ⇒ 斜辺=√2」になります。
ア~カの中から,二等辺三角形を3つ選んで,記号をかきなさい。 ( イ ) ( エ ) ( オ ) 2 2~4について, 空欄をうめて,証明を完成させなさい。 2つの角が等しい三角形は,二等辺三角形である (二等辺三角形の条件) 証明 頂角aの二等分線adをひくCは三角形の3辺の長さであり,さらに,最大辺の長さがaとしてい るので,三角形の成立条件は a < bc となる.直角三角形,鋭角三角形,鈍角三角形のいずれであるかを調べるときに 三角形の成立条件を前提としなければならないのか?T:「『 二等辺三角形になるための条件』といいます. 三角形が二等辺三角形とまだわかっていない ときに使うので『2つの角』と表現します.」 ・黒板の図で生徒に簡潔に説明させる. ・「二等辺三角形になるための条件」とし て黒板に整理する.



フロー 2 5 4 4 直角三角形の合同条件を利用した証明




ae Descubre Como Resolverlo En Qanda
次に, 三角形の合同条件(3 辺相等) が成り 立てば,2 つの三角形は合同であることの証明 について述べる。この証明は, 二等辺三角形 の底角定理を使って以下のように証明するこ とができる。 (証明) abc と dce において,ab=de, bc=ef, ca=fd ならば abc ≡ def1 二等辺三角形の2つの底角は等しい。 2 二等辺三角形の頂角の二等分線は底辺を垂直に二等分する。 3 二辺の長さが等しい三角形は二等辺三角形である。 しろのしろたん 3年以上前 とても丁寧にありがとうございます😊💕 もし、「2角の大きさがが間 ・ 二等辺三角形の2つの底角が等しいことを証明することができる。 ・ 定義、頂角、底辺、底角の意味を理解する。 教科書108、109ページの「とびらの問題」の名札立てをつくり、様々な三角形を見付け、それがどのような三角形であるかを示させる




中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット




二等辺三角形と証明 Youtube
② 二等辺三角形の頂角の二等分線は底辺を垂直に二等分する。 ③ 二辺の長さが等しい三角形は二等辺三角形である。 直角三角形 合同条件 ① 斜辺と1つの鋭角がそれぞれ等しいとき、2つの直角三角形中津市立東中津中学校2年数学「三角形」二等辺三角形になる条件 河野秀男教諭 Tweet 印刷用ページを表示する 掲載日:18年7月19日更新 学力向上支援教員・指導教諭らによる優れた授業をお届けする「シリーズ授業まるごと!二等辺三角形の底角が等しいという性質を利用する △DBCはDB=DCの二等辺三角形なので∠DCB=∠DBC=25° 三角形の外角はそれと隣り合わない2つの内角の和に等しいので∠ADB=50° △ABDはAD=ABの二等辺三角形なので∠ADB=∠ABD=50°




二等辺三角形の2つの角は等しくなる ことの説明 おかわりドリル
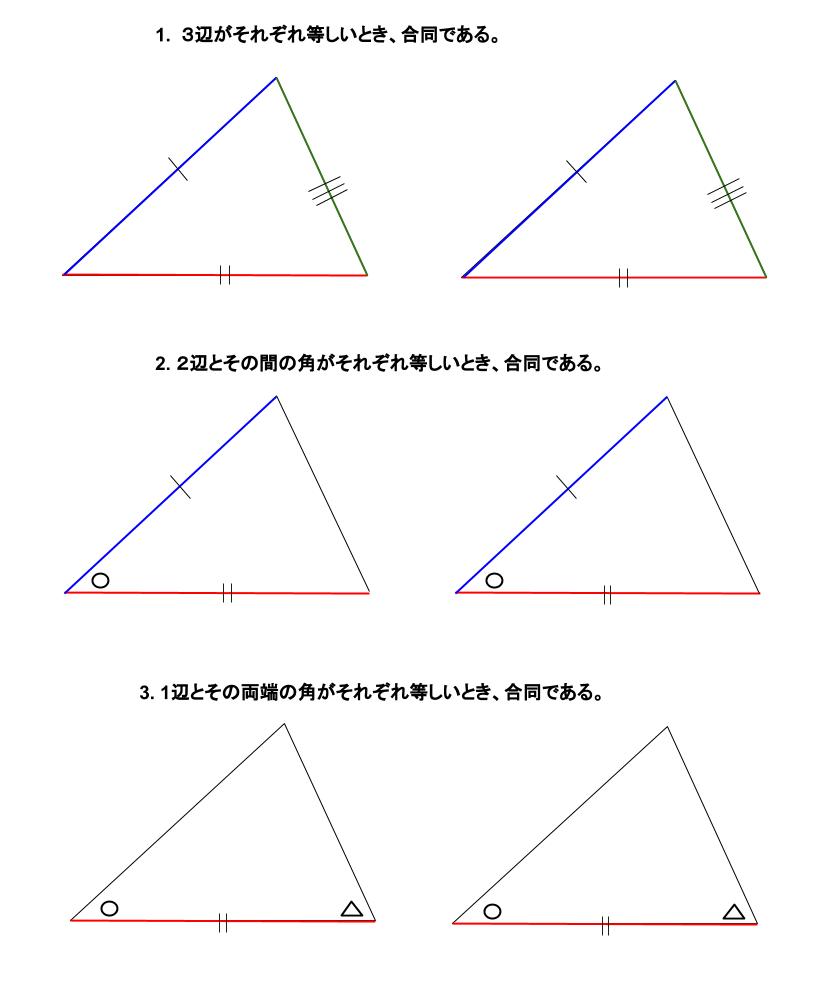



中学数学 三角形の合同条件 中学数学の無料オンライン学習サイトchu Su
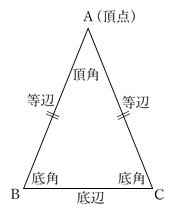
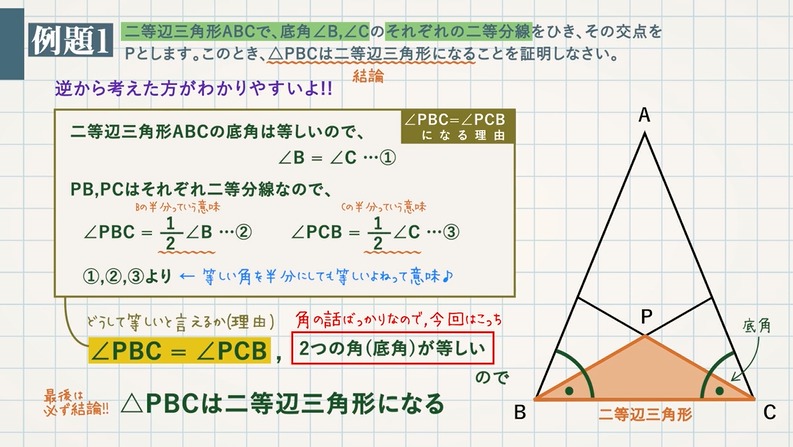
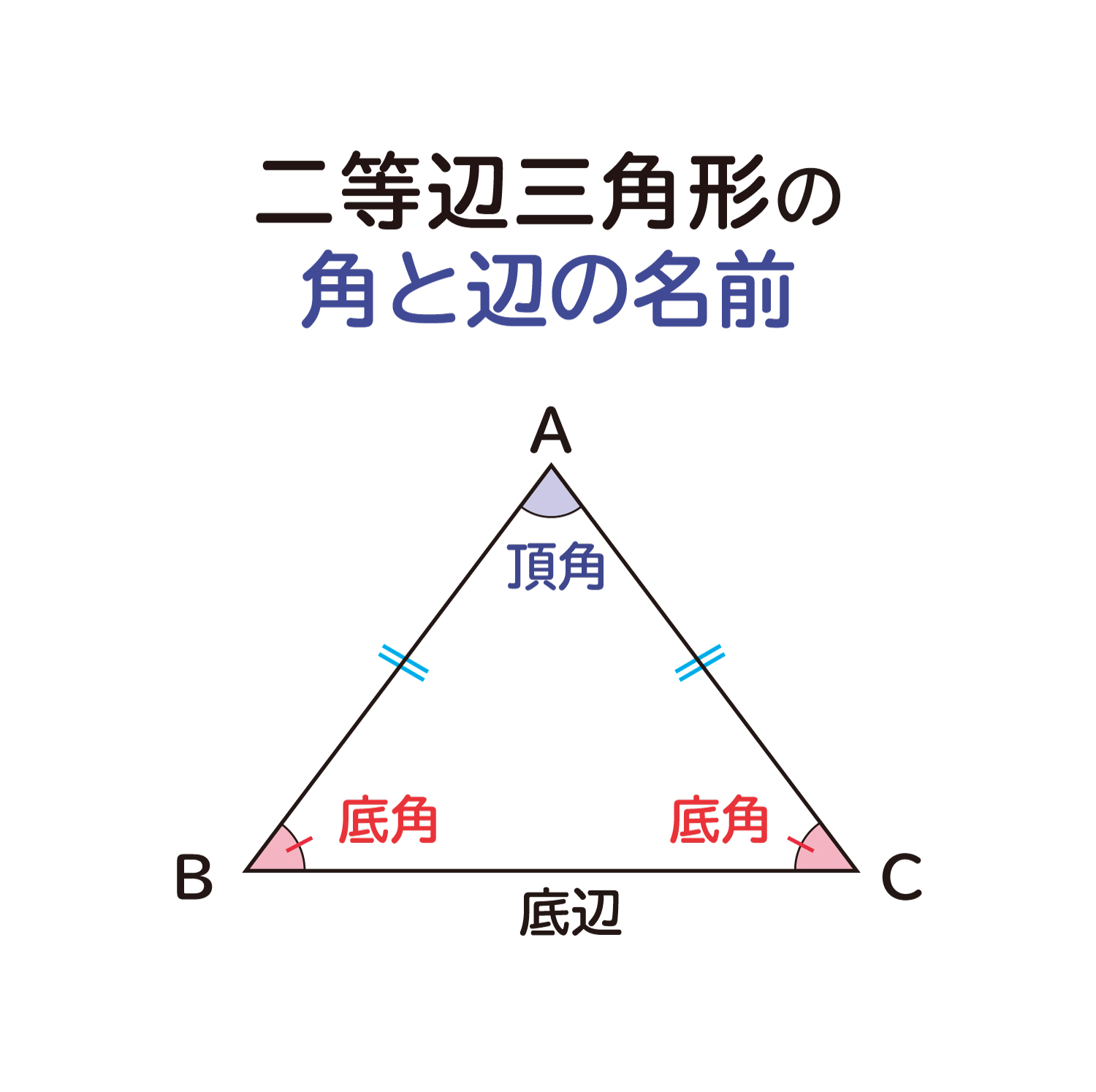
三角形の成立条件の証明(必要性) 「三角形が成立する→三角不等式が成立する」を証明します。 寄り道した方が距離が長くなる という直感に従うと自明ですが,一応きちんと証明して1 : 2 つの底角は愛しい 2 :頂角の二等分線は、底辺を垂直に二等分する 二等辺三角形になるための条件 (定義と定理を使う) ・ 2 辺が等しい ・ 2 つの角 (底角)が等しい このどちらかを証明できれば、二等辺三角形だと言えます。 1:23 例題 1 二2 つの辺が等しい三角形を二等辺三角形という(定義 ていぎ)。 右図のようなab=ac の二等辺三角形で, ∠aを 頂角 ちょうかく ,頂角に対する辺bcを底辺 ていへん , 底辺の両端の∠bと∠cを 底 てい 角 かく という。 問題(後期期末)




相似15 二等辺三角形 Youtube
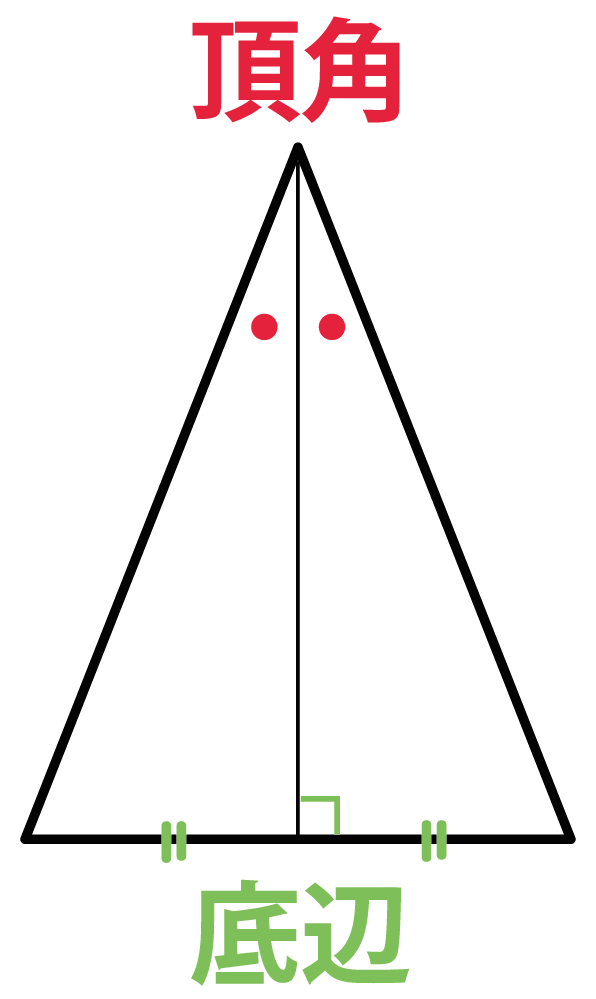



3分でわかる 二等辺三角形の2つの定理 性質 Qikeru 学びを楽しくわかりやすく
赤い部分が二等辺直角三角形になるのはなぜ? 教員採用試験の問題集にあり、恥ずかしながら自分にはわからなかったので質問です。 正方形の中に、正三角形が図のように内接しているとします。 そのとき、赤い三二等辺三角形の頂角の二等分線は, 底辺を垂直に2 等分する さが等しい 1組の対辺が平行でその長 四角形は、平行四辺形 2つの角が等しい三角形は、その 角を底角とする二等辺三角形 定義 長方形 4つの角がすべて等しい四角形 正三角形 定義3つの 二等辺三角形とは?定義 二等辺三角形とは、 \(\bf{2}\) つの辺の長さが等しい三角形 のことです。 二等辺三角形の等しい \(2\) 辺の間の角のことを「頂角」、その他の \(2\) つの角のことを「底角」といいます。そして、頂角に向かい合う辺のことを「底辺」といいます。
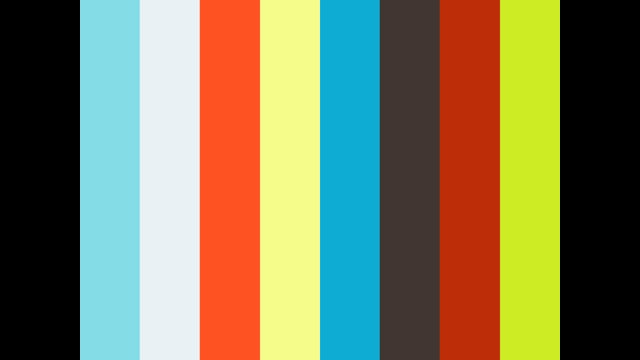



2 57第4章 二等辺三角形 二等辺三角形になるための条件 フロントエンドなブログ
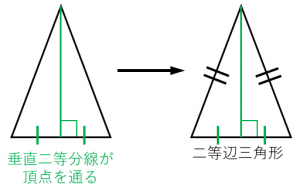



二等辺三角形の4つの性質と4つの条件 具体例で学ぶ数学
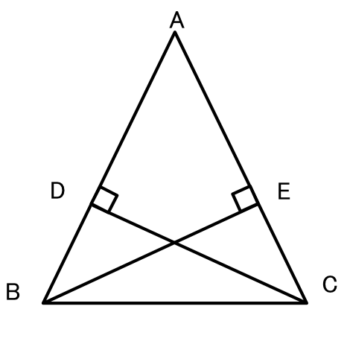
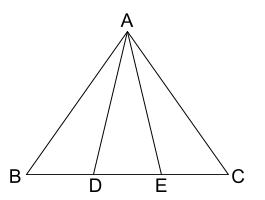
三角形の合同条件 →ふたつの三角形をbcとb'c'が重なるように並べる→aa'の線を引くと aba'と aca'は二等辺三角形→底辺が等しい→∠a=∠a'→二辺夾角が等しいことから、 abc≡ a'b'c' 二等辺三角形の定理(パッポスの証明) 二等辺三角形の場合も、先ほど示した 一般的な三角形の合同条件 を使います。 ただし、 等しい つの底角をもつ頂点は、どちらとどちらを対応させても構いません 。 三角形の3つの内角の和は180°だから、∠a=∠d=180°―(60°+ア)=イ③ ①②③から、ウがそれぞれ等しいので、 abc≡ def 6ab=acの二等辺三角形abcで、頂点bから辺acに垂線をひき、その交点をeとします。このとき、ad=aeになることを証明しなさい。




二等辺三角形 直角三角形の定義 合同条件と証明問題 リョースケ大学
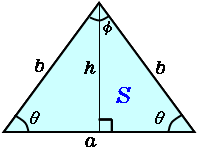



二等辺三角形 高精度計算サイト
\(\triangle ABC\) が二等辺三角形であることを証明せよ 三角形が二等辺三角形であることを示したいとき、 ・\(2\) つの辺が等しい ・\(2\) つの角が等しい のどちらか片方がいえればOKです。 これも暗記ですよ。 三角形の合同条件を暗記したの同じように。 例題1




定理 二等辺三角形の両底角は等しい を使って 身勝手な主張
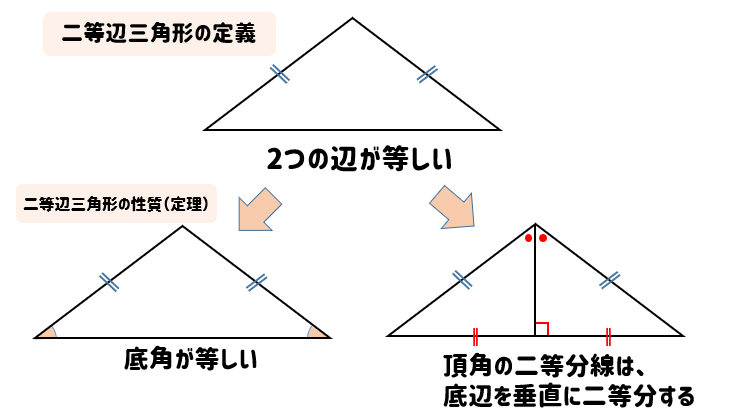



二等辺三角形の定義と性質をサクッと確認しておこう 数スタ



3年算数三角形教え方のポイント




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ



三角形の合同条件と二等辺三角形の底角 2 算数 数学記事




中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン



三角形 四角形 おやじさん ネット




直角二等辺三角形 Wikipedia




簡単公式 直角二等辺三角形の面積の2つの求め方 Qikeru 学びを楽しくわかりやすく




直角三角形の合同条件とその証明 数学fun




3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ




二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者




頂角36度の二等辺三角形の辺の比を教えてください 頂角36度の二等辺三 数学 教えて Goo




二等辺三角形になることの証明 Youtube




中2数学 二等辺三角形の性質2 頂角の二等分線 練習編 映像授業のtry It トライイット



直角三角形の合同条件 証明問題の書き方とは イチから徹底解説 数スタ




二等辺三角形の定理の証明がわかる3ステップ Qikeru 学びを楽しくわかりやすく




國二 Junior High数学的 数学 中2 定義と定理 筆記 Clear
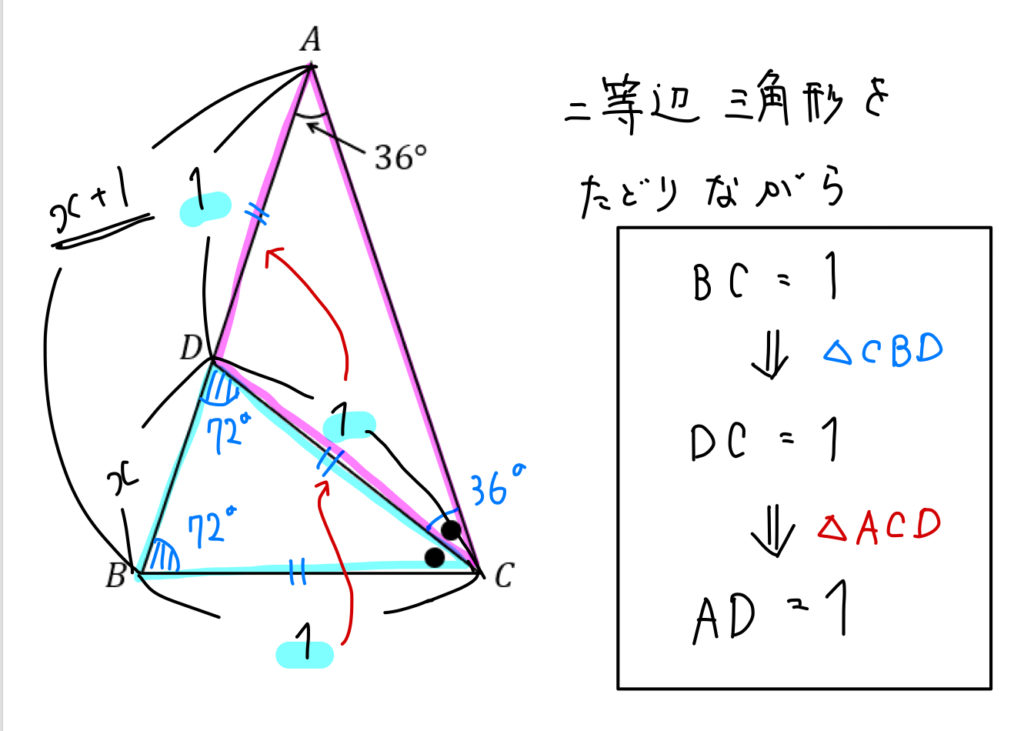



数学 36 の三角比 二等辺三角形を用いて求める方法は 数スタ




中2数学 二等辺三角形の証明 例題編 映像授業のtry It トライイット
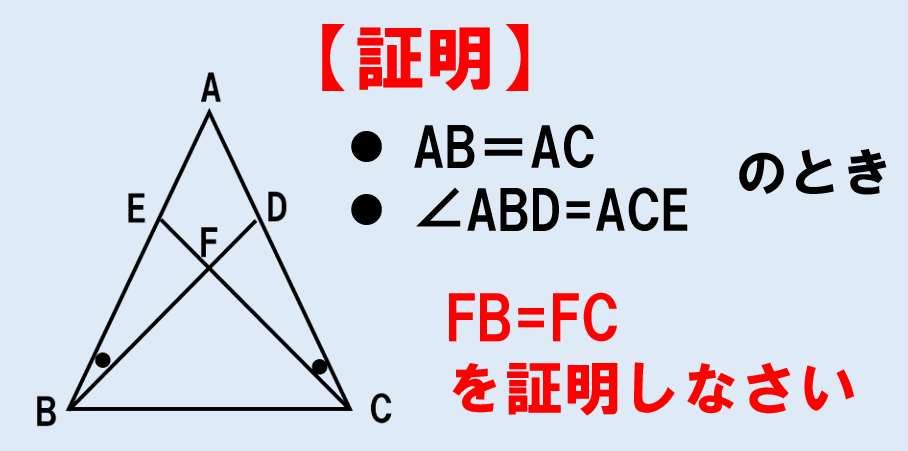



中2数学 2角が等しい三角形 二等辺三角形の長さを用いた証明 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト




二等辺三角形の定理の証明がわかる3ステップ Qikeru 学びを楽しくわかりやすく



1



3




二等辺三角形の定理や性質 底角が等しいことは絶対に覚えよう 中学や高校の数学の計算問題




二等辺三角形の性質 Youtube




二等辺三角形と正三角形 算数用語集
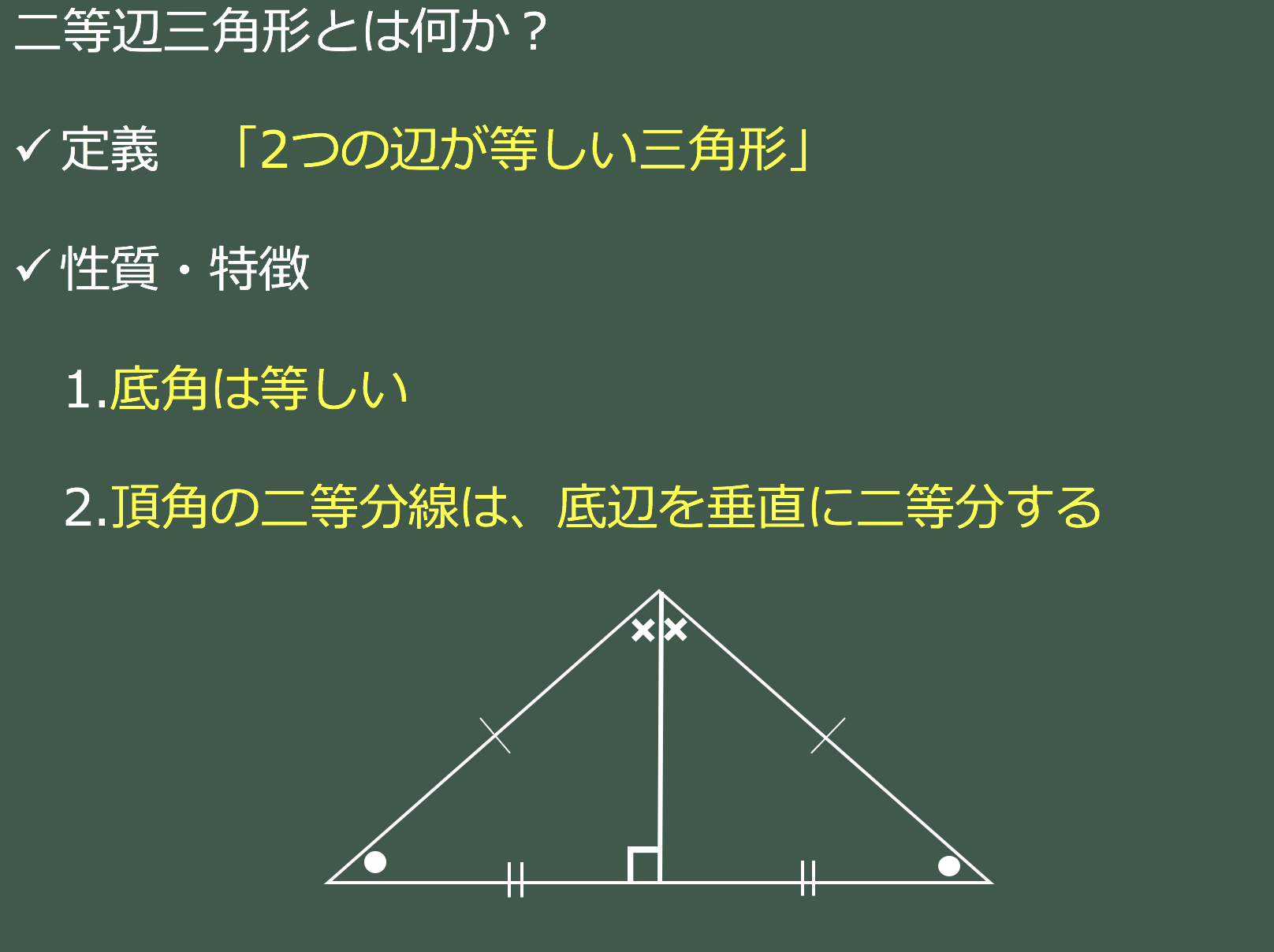



3分で分かる 二等辺三角形の特徴 角度 辺など についてわかりやすく 合格サプリ
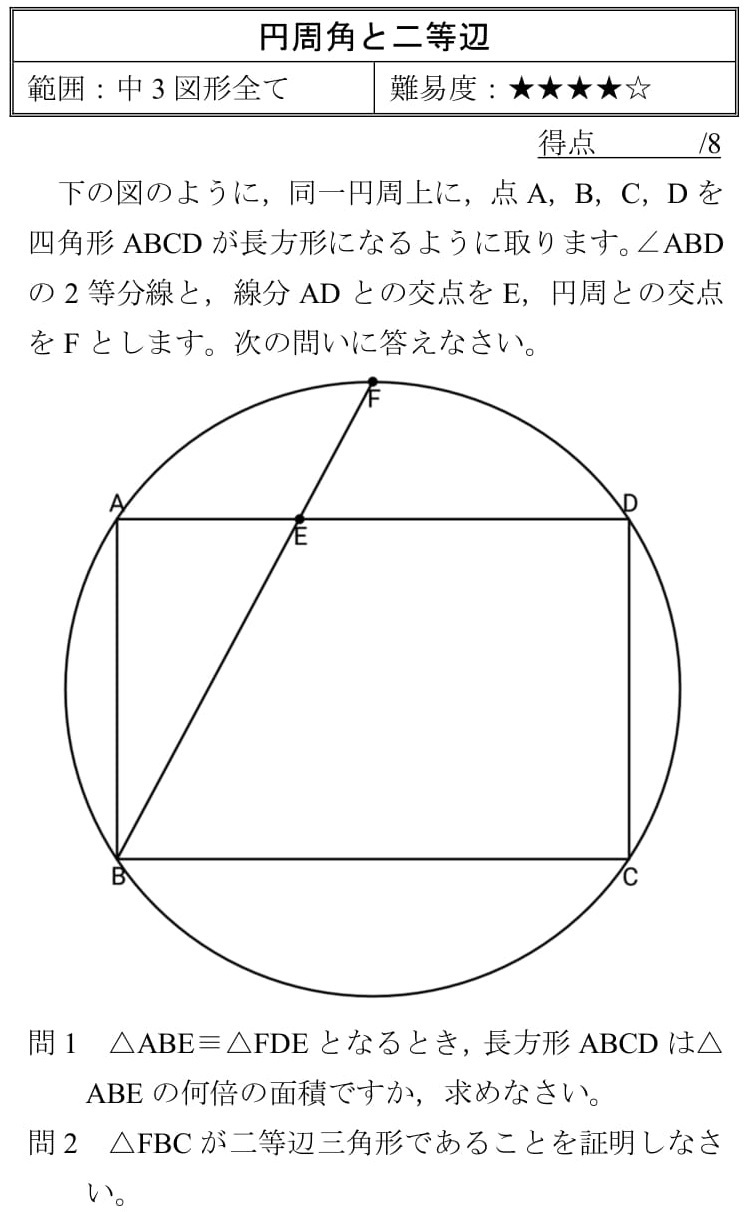



円周角と二等辺三角形 オリジナル 高校入試 数学 良問 難問
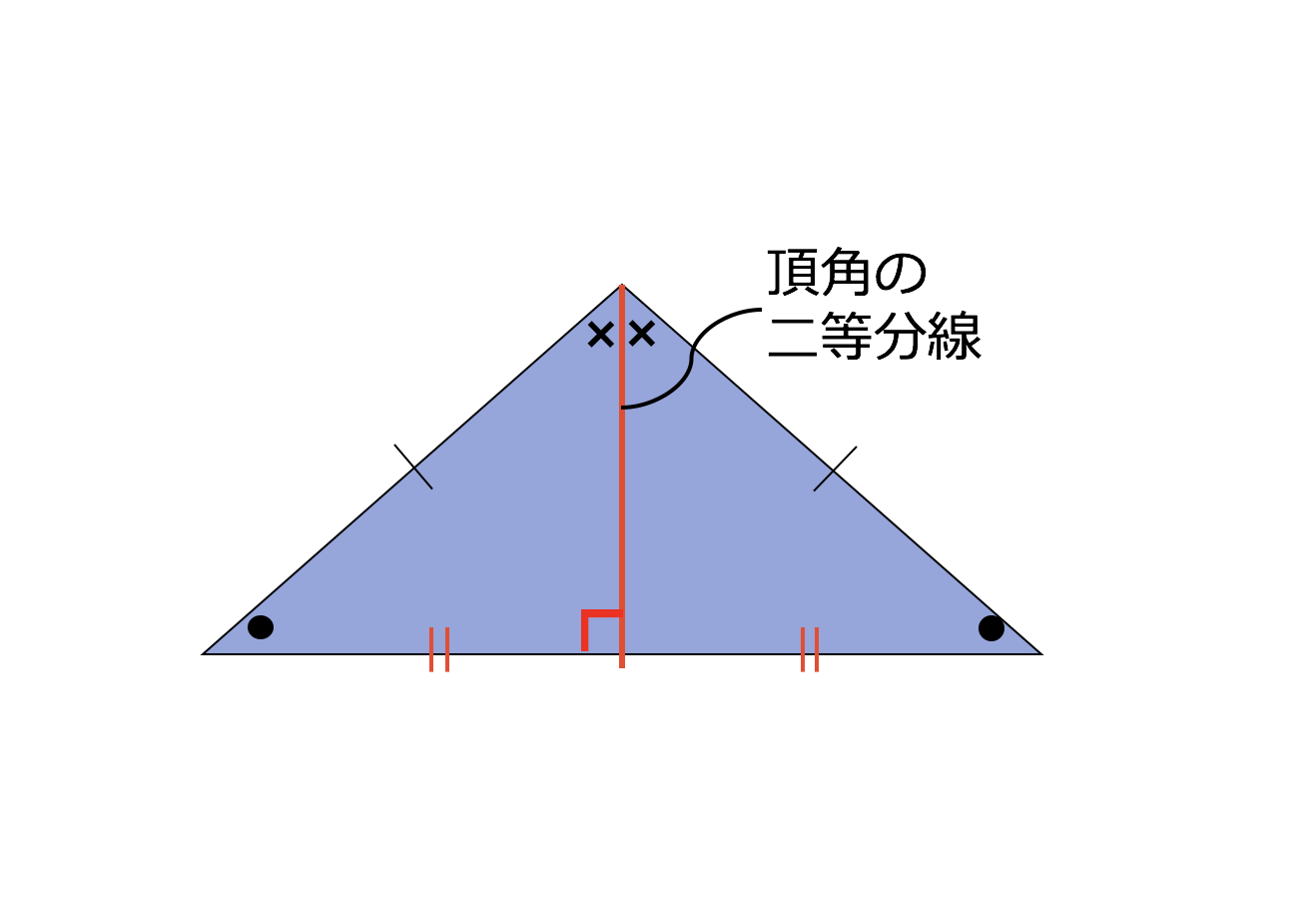



3分で分かる 二等辺三角形の特徴 角度 辺など についてわかりやすく 合格サプリ



数学 二等辺三角形になるための条件 タイトル この問題 Yahoo 知恵袋




二等辺三角形の性質と証明 無料で使える中学学習プリント



二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者



直角三角形の合同条件とそれを利用した証明 チーム エン



二等辺三角形の4つの性質と4つの条件 具体例で学ぶ数学




Tossランド 二等辺三角形になるための条件



二等辺三角形の4つの性質と4つの条件 具体例で学ぶ数学



合同な図形 二等辺三角形の証明問題 苦手な数学を簡単に




この3問がどうしても わかりません 回答お願いいたします もしよければ途中経過も Clear
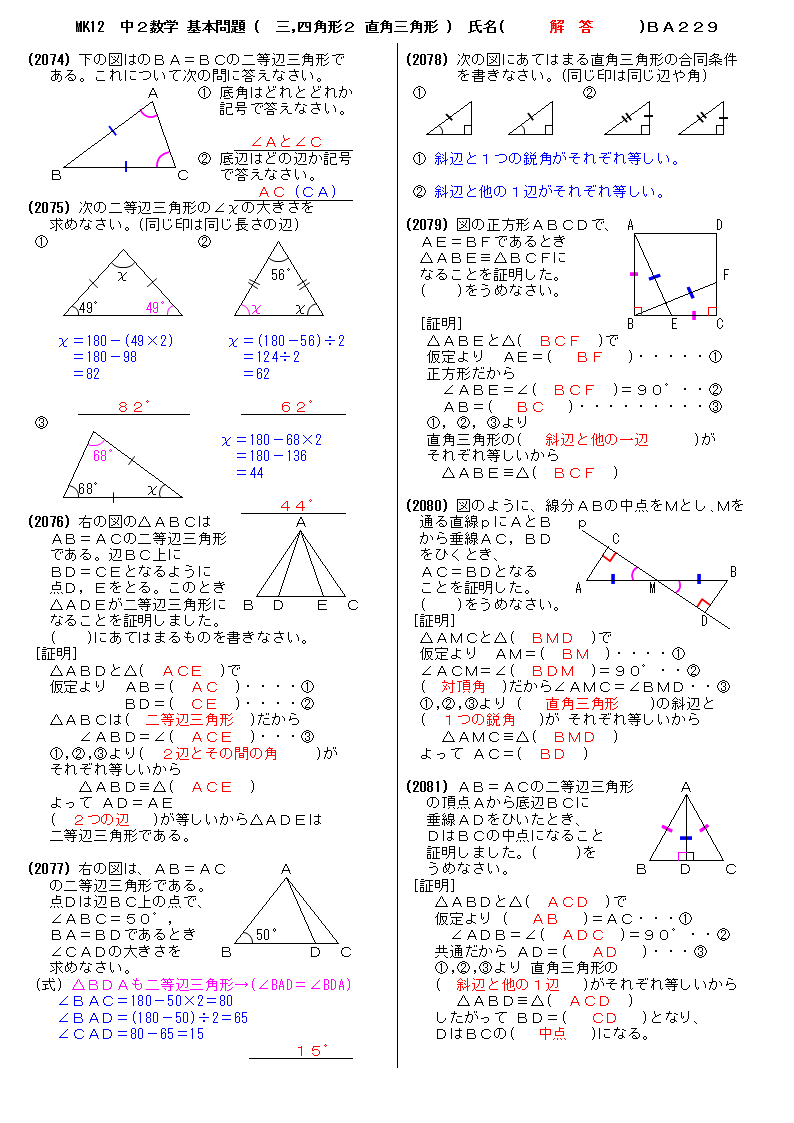



無料 中2数学 基本問題 解答プリント 229 三角形 四角形2 直角三角形
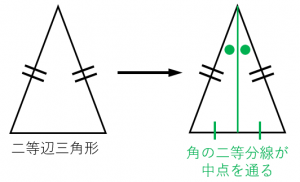



二等辺三角形の4つの性質と4つの条件 具体例で学ぶ数学




直角三角形の合同条件を使った証明とは なぜ2つ増えるのか 遊ぶ数学
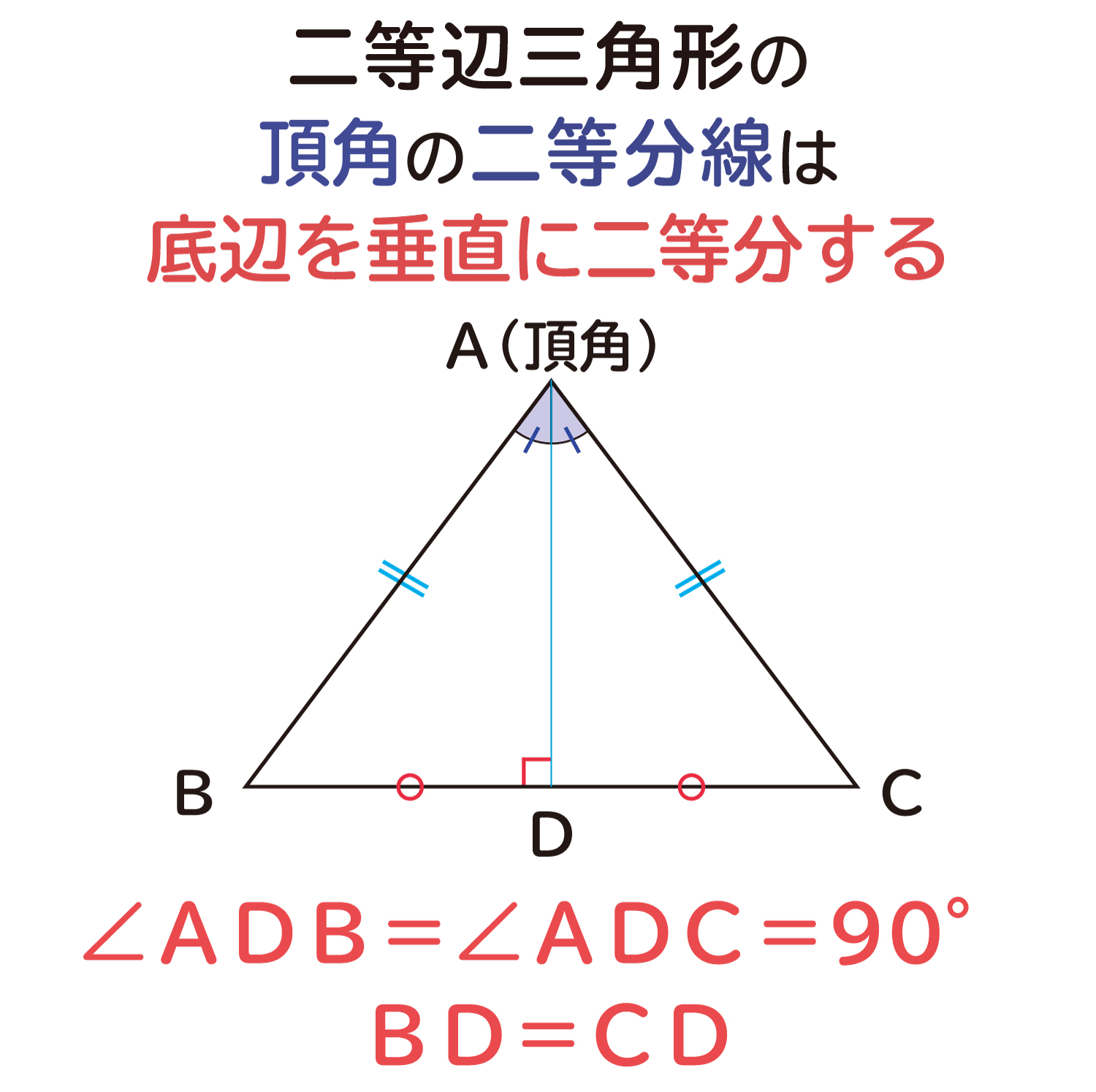



二等辺三角形の頂角の二等分線は 底辺を垂直に二等分する ことの説明 おかわりドリル




โน ตของ 二等辺三角形になるための条件 ช น Junior High数学 Clear




二等辺三角形に関するある問題 底辺 高さそして面積 身勝手な主張




二等辺三角形の定義 角度の性質を使った証明問題などを解説 遊ぶ数学




中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット




三角形の成立条件を理解するたった1つのポイント わかりやすく解説 遊ぶ数学




世界一わかりやすい数学問題集中2 5章 図形の性質と証明
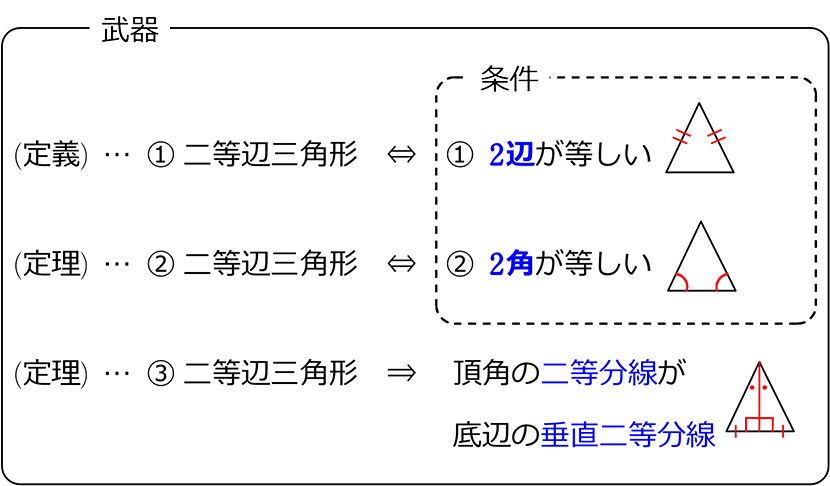



中学数学 図形の合同 図形の性質




二等辺三角形の性質の証明 中学数学 By Okボーイ マナペディア
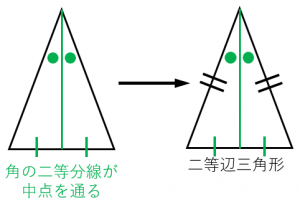



二等辺三角形の4つの性質と4つの条件 具体例で学ぶ数学



二等辺三角形ができる条件
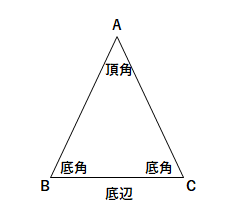



中2数学 二等辺三角形の定義と性質 Examee
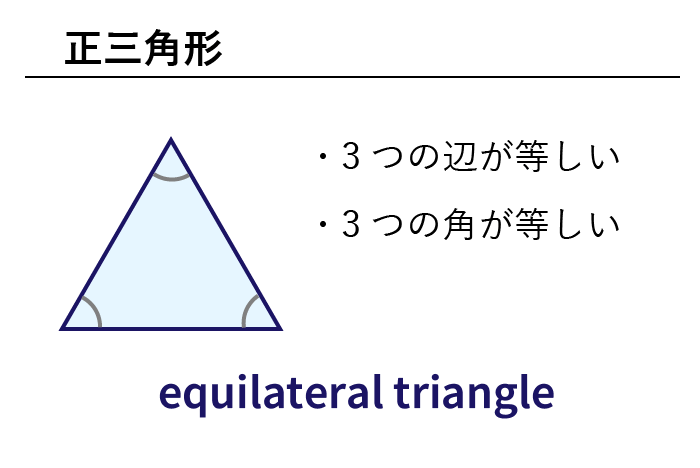



数学 色々な三角形の英単語まとめ 二等辺三角形 直角三角形ほか 英単語project




二等辺三角形の底角は本当に等しいのか ひと筋縄ではいかない証明 ブルーバックス編集部 ブルーバックス 講談社 1 4
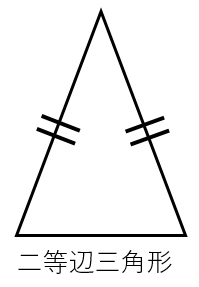



二等辺三角形の4つの性質と4つの条件 具体例で学ぶ数学



二等辺三角形とは 定義や定理 角度 辺の長さ 面積の求め方 受験辞典



二等辺三角形と頂角の二等分線の性質を証明 底角は必ず鋭角になるのか まぜこぜ情報局
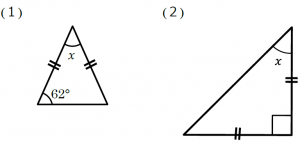



中2数学 図形の中でも重要なものの1つ 二等辺三角形について徹底解説 まなビタミン
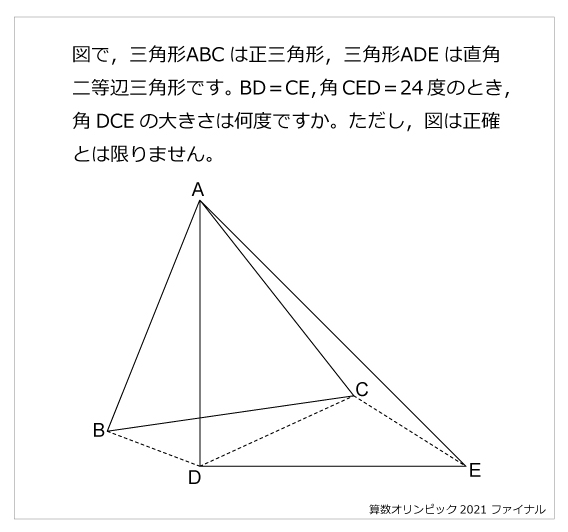



直角二等辺三角形 算数星人のweb問題集 中学受験算数の問題に挑戦



1
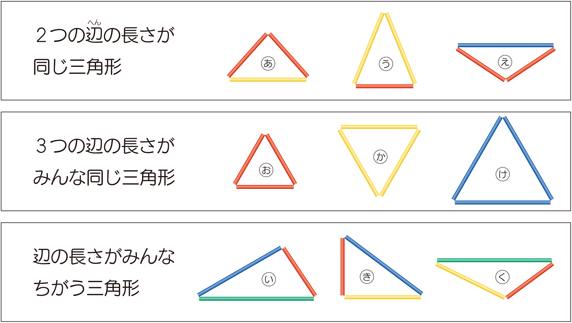



二等辺三角形と正三角形 算数用語集



二等辺三角形の2つの角は等しくなる ことの説明 おかわりドリル



二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者




二等辺三角形 Wikipedia



Http Cms Oklab Ed Jp Jh Rokuhoku Index Cfm 1 1423 C Html 1423 1217 Pdf



数学 相似条件と証明 について 下の図 写真 で Abcは Ab Yahoo 知恵袋



中学数学 証明 二等辺三角形の性質の利用 中学数学の無料オンライン学習サイトchu Su




二等辺三角形の定理の証明がわかる3ステップ Qikeru 学びを楽しくわかりやすく



1




二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者



二等辺三角形の定義と性質 問題の解き方 数学fun



斜辺10cm 高さ6cmの ありえない 直角三角形の面積を真面目に求める
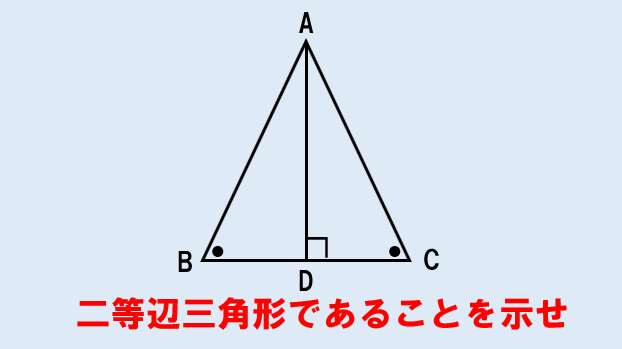



中2数学 二等辺三角形の証明問題 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト




中2 二等辺三角形の性質 中学生 数学のノート Clear




スタディピア 図形



中学数学証明問題です 直角三角形の合同条件はわかるのですが Yahoo 知恵袋




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ
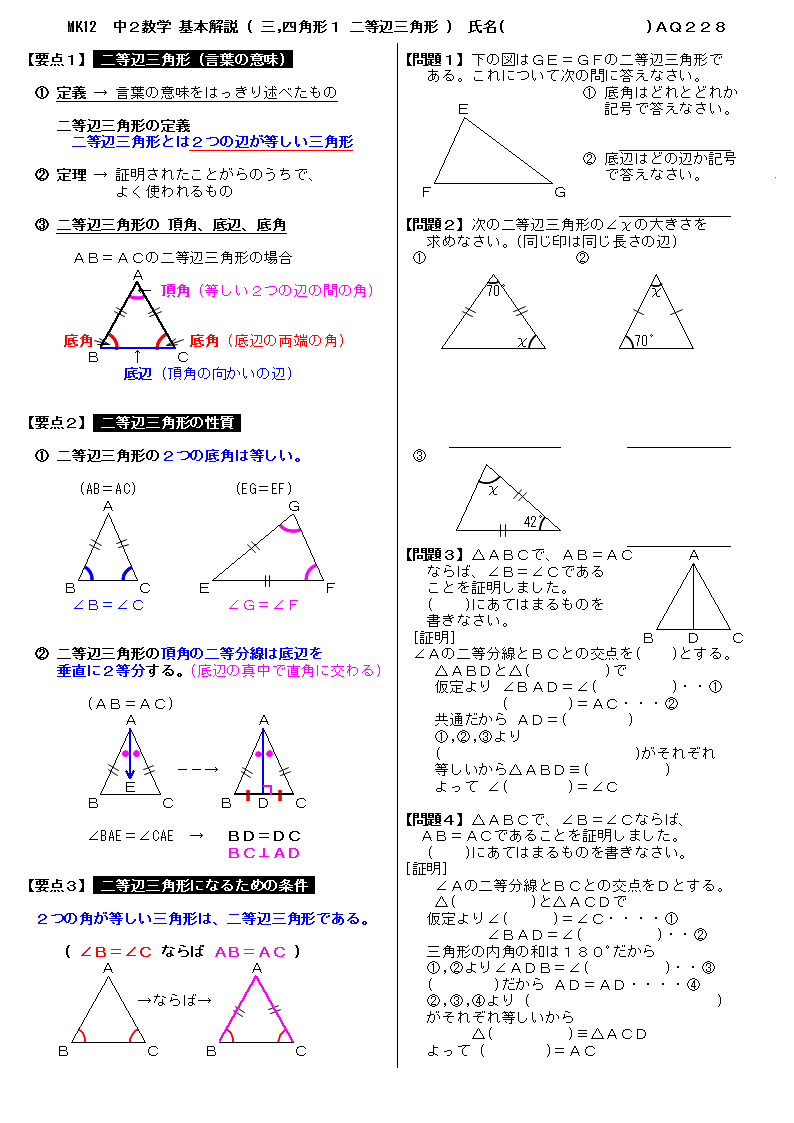



無料 中2数学 基本解説 問題プリント 228 三角形 四角形1 二等辺三角形




中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット




この問題の仮定と結論ってどれですか あと 解き方 教えてください Clear
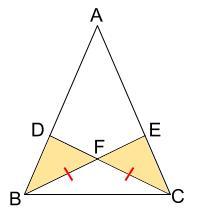



中学数学 証明 二等辺三角形であることの証明 中学数学の無料オンライン学習サイトchu Su




二等辺三角形になるための条件 Youtube



三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典




中高生必読 知らないとヤバい二等辺三角形の知識 定義 角度 面積 高校生向け受験応援メディア 受験のミカタ




中学2年生の数学 証明 二等辺三角形と直角三角形 塾講師が数学をやりmath



直角二等辺三角形とは 定義や辺の長さの比 面積の求め方 受験辞典




二等辺三角形になるための条件 Youtube




二等辺三角形と証明 Youtube




ae Descubre Como Resolverlo En Qanda
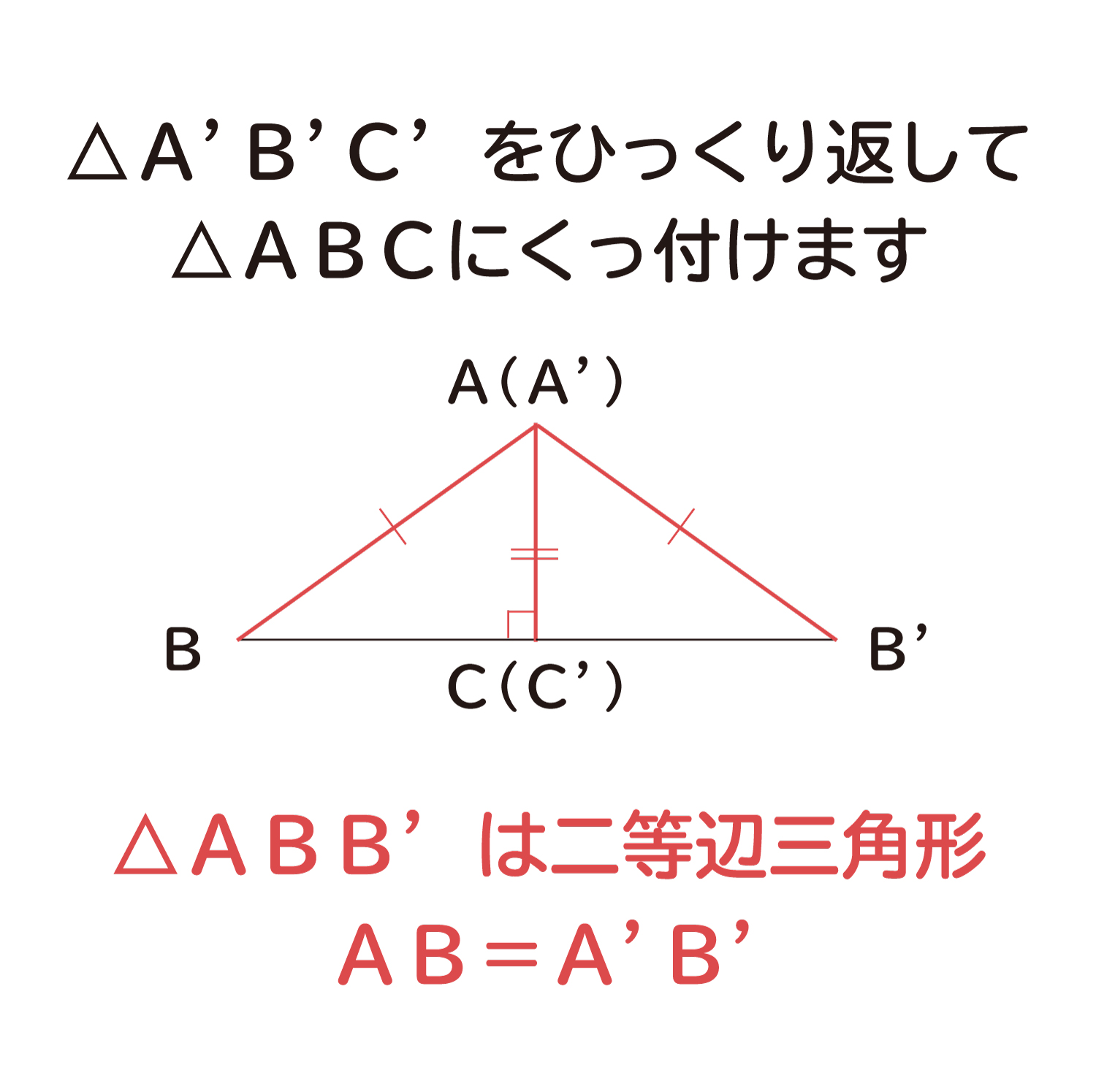



直角三角形の合同条件の説明 おかわりドリル



0 件のコメント:
コメントを投稿