
この問題の違いを教えてください つけるのと付けないのがありますよね Clearnote
これは、54の平方根が73と74の間にあることを意味します。 別の例を見てみましょう。 例: 27の平方根とは何ですか? 解決: 27はどんな数の完全な二乗でもないので。したがって、次のように単純化する必要があります。 √27=√9* 3 √9*√3=3√3The decimal expansion of √2
4の平方根とは
4の平方根とは- 平方根とは ここでは、平方根とはどんな考え方をしているのか、 どのように表すのかなどの基本的な内容を扱っていきます。 基礎から見直したいという方はこちらから読み始めてください! 平方根の考え方 平方根とは2乗の逆のことです!Xを解きます x9=4の平方根の自然対数 ln (√x 9) = 4 ln ( x 9) = 4 x x を解くには、対数の性質を使い方程式を書き換えます。 eln(√x9) = e4 e ln ( x 9) = e 4 指数と対数は逆関数の関係です。 √x9 = e4 x 9 = e 4 x x を解きます タップしてもっと手順を表示する
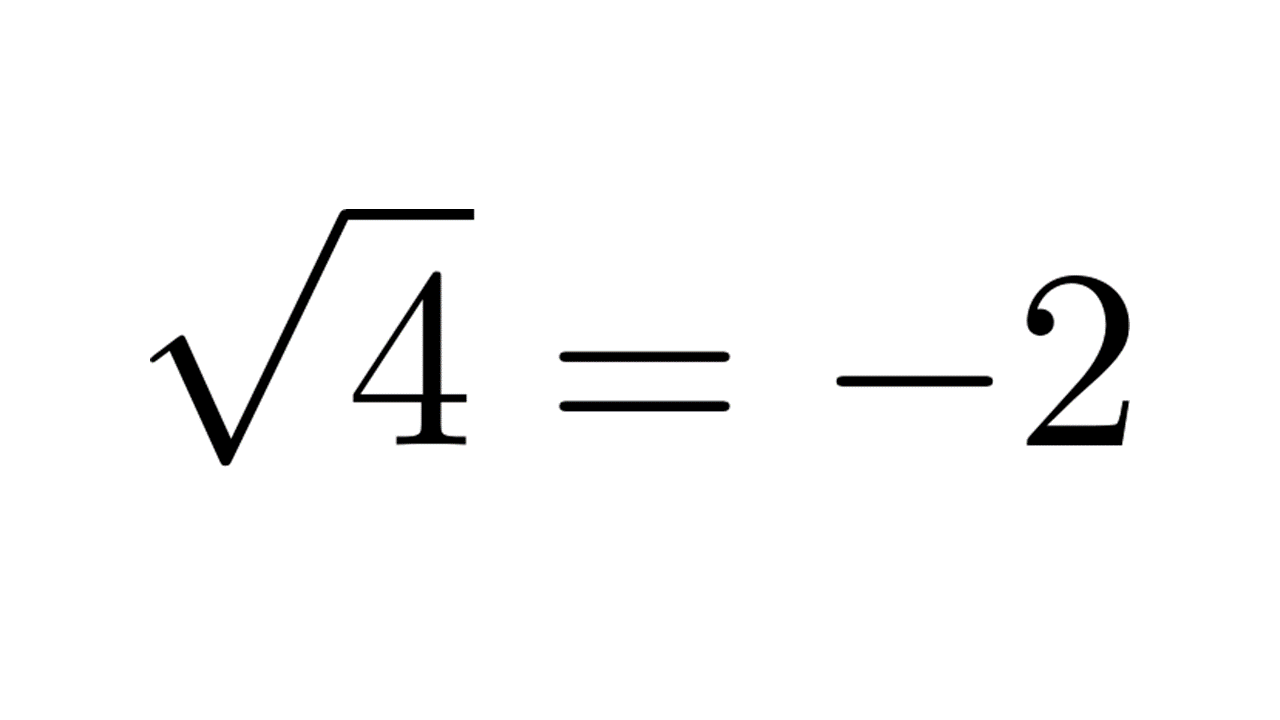
Sqrt 4 2 を実感する 多価関数への誘い 数学 統計教室の和から株式会社
正の数 ⇒ 平方根は正と負の2つ 0 ⇒ 0の平方根は0だけ 負の数 ⇒ 平方根は存在しない 文字のときの平方根 ( ) 2 =x 4 となるのは にx 2 または−x 2 が入るとき。 つまりx 4 の平方根は±x 2 である。 確認次の数の平方根を求めよ。上記のほかに、3は平方根ですか? 3の平方根は正の実数であり、それ自体を掛けると3になります。数学的には√3で表されます。 同じプロパティを持つ負の数と区別するために、より正確には3の主平方根と呼ばれます。 3の平方根は無理数ですSo 2 root 2 is an irrational number Similarly, Is Root 2 a irrational number?
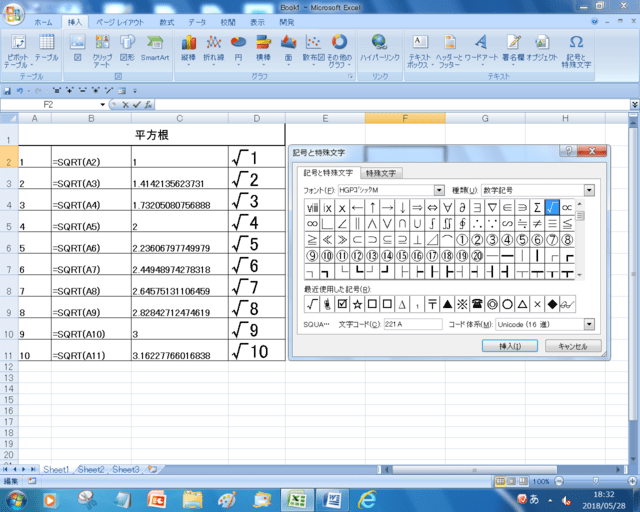
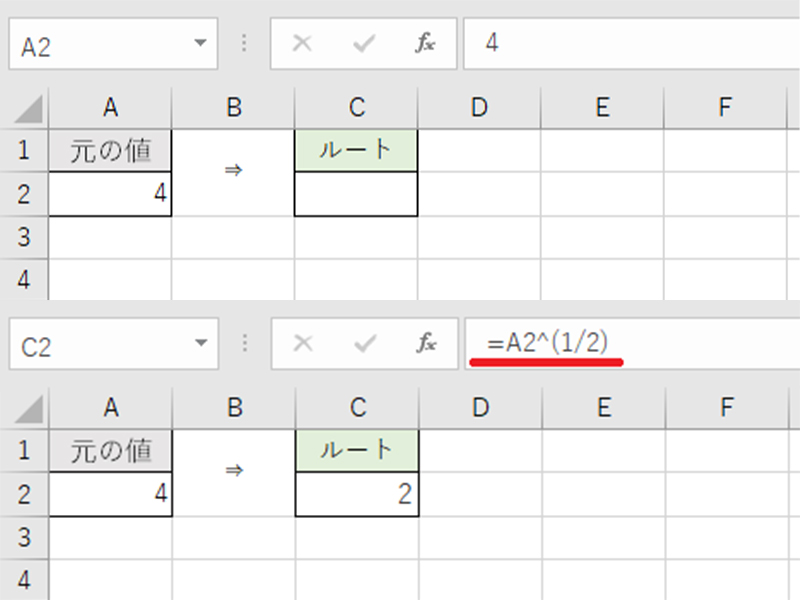
平方根とは? 平方根は、 「ある数 を2乗すると となるとき、その を の 平方根 という」 と定義されているものです。 文章を読むだけでは正直よくわかりませんね。 しかし、平方根の考え方自体には既に触れてきています。 正方形の面積と辺の長さの0 の平方根は 0 (のみ)であり,0以外の平方根は正および負で,絶対値が等しい 2つの数になります。例えば,2の平方根は\(\pm\sqrt{2}\)であり,4の平方根は \(\pm2\) です。 ここで例示した4の平方根は\(\pm2\)であるということは,問題なく納得できると思いますが この数字を、平方根を示す√(ルート)の記号を使って表すと、√xとなります。 具体的な数字を挙げて考えてみましょう。 例えば、4は2を2回かけることによって4になるため、4の平方根は次のように考えられます。 √4=2 そして、以下のように計算する
4の平方根とはのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |
 中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |
 中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |
「4の平方根とは」の画像ギャラリー、詳細は各画像をクリックしてください。
中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |
 中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |
 中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote | 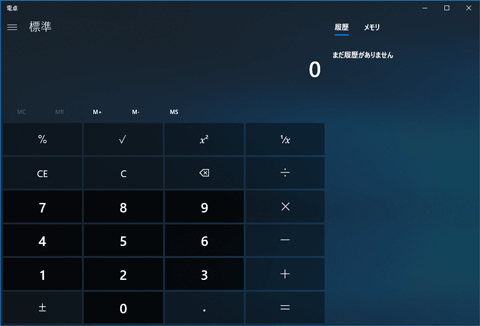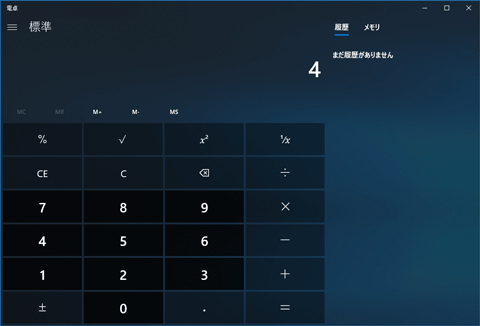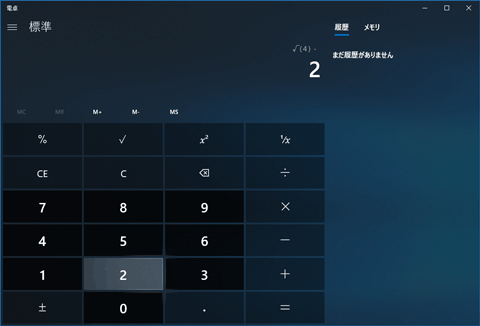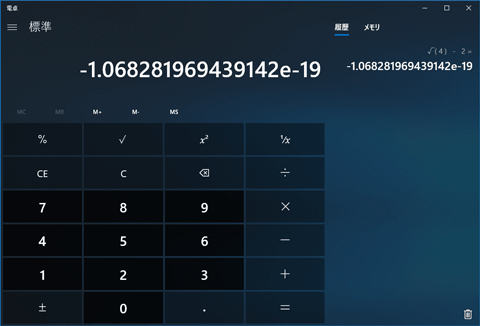 中3の平方根の所です Clearnote |
「4の平方根とは」の画像ギャラリー、詳細は各画像をクリックしてください。
 中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote | 中3の平方根の所です Clearnote |
 中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |
 中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote | 中3の平方根の所です Clearnote |
「4の平方根とは」の画像ギャラリー、詳細は各画像をクリックしてください。
 中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |
 中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |
 中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |
「4の平方根とは」の画像ギャラリー、詳細は各画像をクリックしてください。
 中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |
 中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |
 中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |
「4の平方根とは」の画像ギャラリー、詳細は各画像をクリックしてください。
 中3の平方根の所です Clearnote | 中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |
 中3の平方根の所です Clearnote | 中3の平方根の所です Clearnote | 中3の平方根の所です Clearnote |
中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |
「4の平方根とは」の画像ギャラリー、詳細は各画像をクリックしてください。
 中3の平方根の所です Clearnote | 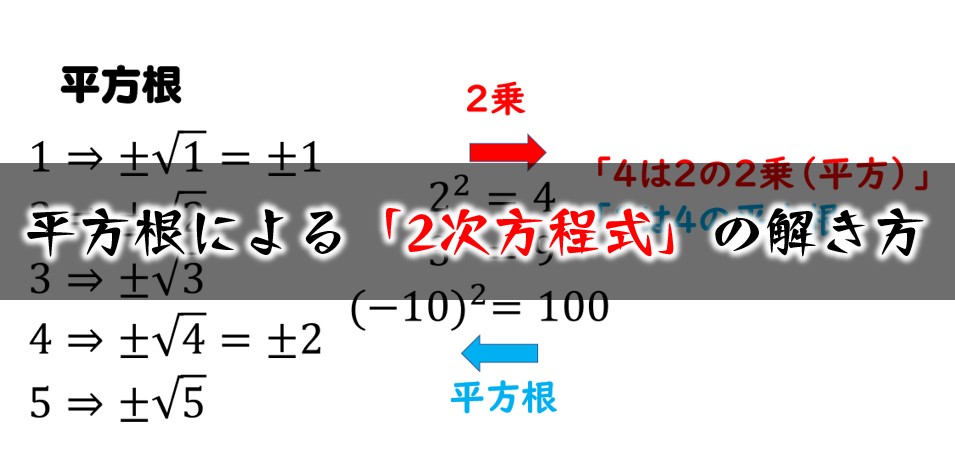 中3の平方根の所です Clearnote | 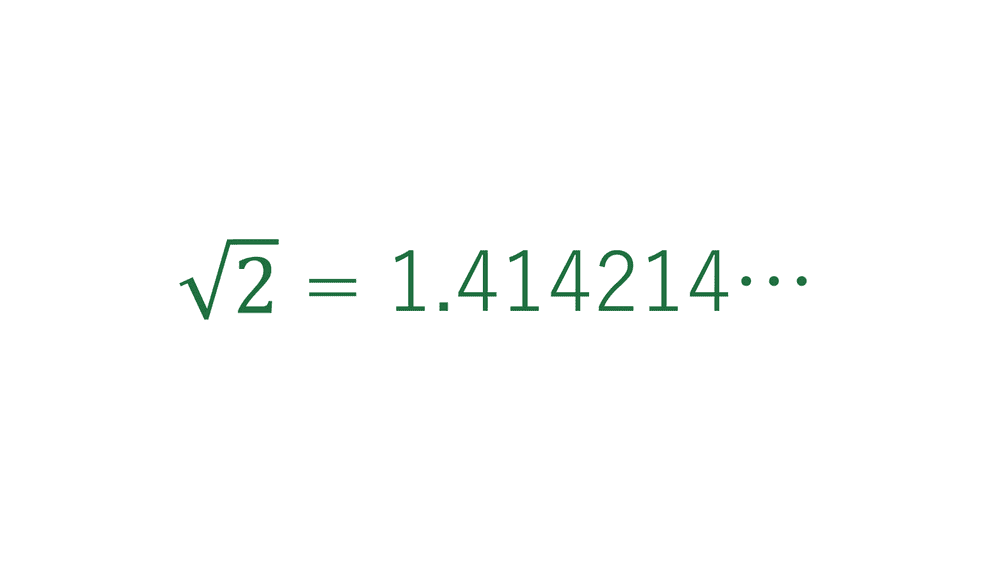 中3の平方根の所です Clearnote |
 中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote | 中3の平方根の所です Clearnote |
 中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote | 中3の平方根の所です Clearnote |
「4の平方根とは」の画像ギャラリー、詳細は各画像をクリックしてください。
 中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |
 中3の平方根の所です Clearnote | 中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |
 中3の平方根の所です Clearnote | 中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |
「4の平方根とは」の画像ギャラリー、詳細は各画像をクリックしてください。
 中3の平方根の所です Clearnote | 中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |
 中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |
 中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |
「4の平方根とは」の画像ギャラリー、詳細は各画像をクリックしてください。
 中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |
 中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |
中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |
「4の平方根とは」の画像ギャラリー、詳細は各画像をクリックしてください。
 中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |
 中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |
 中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |
「4の平方根とは」の画像ギャラリー、詳細は各画像をクリックしてください。
 中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |  中3の平方根の所です Clearnote |
中3の平方根の所です Clearnote | 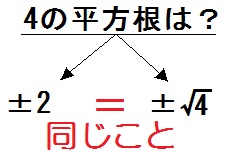 中3の平方根の所です Clearnote |
平方根が整数となる条件は √ A 2 の形で表せること. 検索キーワード: 平方根, 整数問題, √00−5n 00 − 5 n, 整数, 自然数, n n, 何個.4 (x 項の係数) を 2 で除算して 2 を求めます。次に、方程式の両辺に 2 の平方を加算します。この手順により、方程式の左辺が完全平方になります。





0 件のコメント:
コメントを投稿